题目内容
已知:函数y=ax2﹣(3a+1)x+2a+1(a为常数).
(1)若该函数图象与坐标轴只有两个交点,求a的值;
(2)若该函数图象是开口向上的抛物线,与x轴相交于点A(x1,0),B(x2,0)两点,与y轴相交于点C,且x2﹣x1=2.
①求抛物线的解析式;
②作点A关于y轴的对称点D,连结BC,DC,求sin∠DCB的值.
(1)a=0或﹣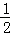 或﹣1;(2)①y=x2﹣4x+3②
或﹣1;(2)①y=x2﹣4x+3②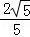 .
.
【解析】
试题分析:(1)分一次函数和二次函数两种情况讨论;(2)①根据题意可得x1,x2为ax2﹣(3a+1)x+2a+1=0的两个根,然后利用根与系数的关系,将x2﹣x1=2进行变形消去x1,x2,,解以a为未知数的方程即可;②根据条件求出点A、B、C、D的坐标,过点D作DE⊥CB于E,可证△EDB为等腰直角三角形,利用勾股定理求出DE、CD的长,根据定义可求sin∠DCB的值.
试题解析:【解析】
(1)函数y=ax2﹣(3a+1)x+2a+1(a为常数),
若a=0,则y=﹣x+1,与坐标轴有两个交点(0,1),(1,0); 1分
若a≠0且图象过原点时,2a+1=0,a=﹣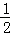 ,有两个交点(0,0),(1,0); 2分
,有两个交点(0,0),(1,0); 2分
若a≠0且图象与x轴只有一个交点时,令△=0有:
△=(3a+1)2﹣4a(2a+1)=0,解得a=﹣1,有两个交点(0,﹣1),(1,0).
综上得:a=0或﹣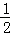 或﹣1时,函数图象与坐标轴有两个交点. 4分
或﹣1时,函数图象与坐标轴有两个交点. 4分
(2)①∵函数与x轴相交于点A(x1,0),B(x2,0)两点,
∴x1,x2为ax2﹣(3a+1)x+2a+1=0的两个根,
∴x1+x2= ,x1x2=
,x1x2=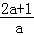 ,∵x2﹣x1=2,
,∵x2﹣x1=2,
∴4=(x2﹣x1)2=(x1+x2)2﹣4x1x2=( )2﹣4
)2﹣4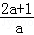 ,
,
解得a=﹣ (函数开口向上,a>0,舍去),或a=1,
(函数开口向上,a>0,舍去),或a=1,
∴y=x2﹣4x+3. 8分
②∵函数y=x2﹣4x+3与x轴相交于点A(x1,0),B(x2,0)两点,与y轴相交于点C,且x1<x2,
∴A(1,0),B(3,0),C(0,3),∵D为A关于y轴的对称点,∴D(﹣1,0).
根据题意画图,
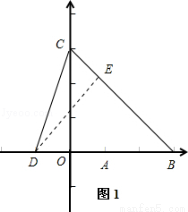
如图1,过点D作DE⊥CB于E,∵OC=3,OB=3,OC⊥OB,∴△OCB为等腰直角三角形,∴∠CBO=45°,∴△EDB为等腰直角三角形,
设DE=x,则EB=x,∵DB=4,∴x2+x2=42,∴x=2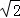 ,即DE=2
,即DE=2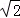 .
.
在Rt△COD中,∵DO=1,CO=3,∴CD=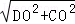 =
=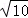 ,∴sin∠DCB=
,∴sin∠DCB=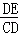 =
=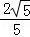 . 14分
. 14分
考点:1.函数与坐标轴的交点;2.一元二次方程根与系数的关系;3.勾股定理;4.三角函数.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案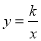 的图象与一次函数
的图象与一次函数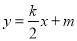 的图象交点为(2,2).
的图象交点为(2,2).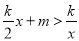 的解集.
的解集.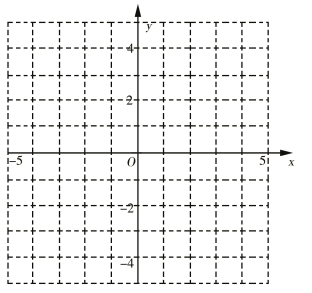

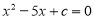 的一个根,则这个方程的另一个根是( )
的一个根,则这个方程的另一个根是( )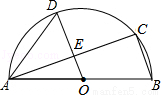
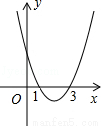
 的倒数为 .
的倒数为 .