题目内容
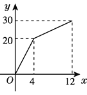
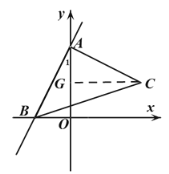
【题目】如图1,在平面直角坐标系中,直线![]() 分别交
分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() ,点
,点![]() ,且
,且![]() 、
、![]() 满足
满足![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)以![]() 为边作
为边作![]() ,点
,点![]() 在直线
在直线![]() 的右侧且
的右侧且![]() ,求点
,求点![]() 的坐标;
的坐标;
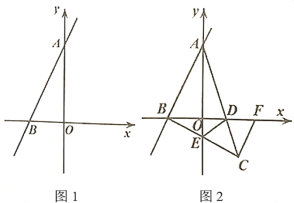
(3)若(2)的点![]() 在第四象限(如图2),
在第四象限(如图2),![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() .
.
①求证![]() ;
;
②直接写出点![]() 到
到![]() 的距离.
的距离.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ;(3)①见解析,②
;(3)①见解析,②![]()
【解析】
(1)将等式![]() 变形后,利用非负数的性质即可得到a,b的值;
变形后,利用非负数的性质即可得到a,b的值;
(2)由题意分![]() 和
和![]() 两种情况讨论,当
两种情况讨论,当![]() 时,过点
时,过点![]() 作
作![]() 于
于![]() ,利用AAS证
,利用AAS证![]() ,从而求得点C的坐标;当
,从而求得点C的坐标;当![]() 时,同理可得解;
时,同理可得解;
(3)①过点![]() 作
作![]() 轴于点
轴于点![]() ,依次证得
,依次证得![]()
![]() ,
,![]()
![]() ,即可得证
,即可得证![]() ;
;
②过点C分别作x轴、DL的垂线,交于点K、H,通过证明△EDC≌△FDC得到∠DEC =∠LEC,再利用角平分线的性质定理得到CH=CL=1.
.解:(1)![]()
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ;
;
(2)由(1)知![]() ,
,![]() ,
,
![]() ,
,![]()
![]() ,
,![]() ,
,
![]() 是直角三角形,且
是直角三角形,且![]() ,
,
![]() 只有
只有![]() 或
或![]() ,
,
Ⅰ、当![]() 时,如图,
时,如图,
![]() ,
,
![]() ,
,
过点![]() 作
作![]() 于
于![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,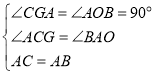
![]()
![]() ,
,
![]() ,
,![]()
![]() ,
,
![]() ,
,
Ⅱ、当![]() 时,如图
时,如图
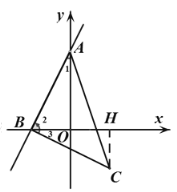
同Ⅰ的方法得,![]() ;
;
即:满足条件的点![]() 或
或![]()
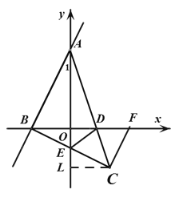
(3)①如图,由(2)知点![]() ,
,
过点![]() 作
作![]() 轴于点
轴于点![]() ,则
,则![]()
在![]() 和
和![]() 中,
中,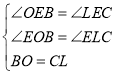
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
![]()
![]() ,
,
![]() ,
,
![]() ;
;
②CH=![]() ,
,
如图,过点C分别作x轴、y轴、DE的垂线,交于点K、L、H,
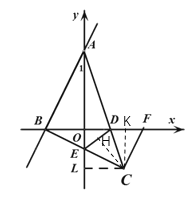
由①可知,CL=CK=1,
∠ECL+∠DCK=∠LCK-∠ECD=90°-45°=45°,
∠FCK+∠KCD=∠ECF-∠ECD=90°-45°=45°,
∴∠ECL=∠FCK,又∠FKC=∠ELC=90°,
∴△ELC≌△FKC(AAS),
∴∠LEC=∠KFC,EC=FC,
∠FCD=∠FCK+∠KCD=∠ECL+∠KCD=45°=∠ECD,
又CD=CD,
∴△EDC≌△FDC(SAS),
∴∠DEC=∠DFC,
∴∠DEC =∠LEC.
又![]()
∴CH=CL=1

练习册系列答案
相关题目