题目内容
矩形ABCD的边AB=3,BC=4,以点B为圆心作圆,使A,C,D三点中至少有一点在⊙B内,且至少有一点在⊙B外,则⊙B的半径r的取值范围是________.
3<r<5
分析:要确定点与圆的位置关系,主要根据点与圆心的距离与半径的大小关系来进行判断.
当d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.
解答: 解:在直角△BCD中CD=AB=3,BC=4,
解:在直角△BCD中CD=AB=3,BC=4,
则BD= =
=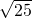 =5.
=5.
由图可知3<r<5,
故答案为:3<r<5.
点评:此题主要考查了点与圆的位置关系,解决本题要注意点与圆的位置关系,要熟悉勾股定理,及点与圆的位置关系.
分析:要确定点与圆的位置关系,主要根据点与圆心的距离与半径的大小关系来进行判断.
当d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.
解答:
 解:在直角△BCD中CD=AB=3,BC=4,
解:在直角△BCD中CD=AB=3,BC=4,则BD=
 =
=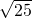 =5.
=5.由图可知3<r<5,
故答案为:3<r<5.
点评:此题主要考查了点与圆的位置关系,解决本题要注意点与圆的位置关系,要熟悉勾股定理,及点与圆的位置关系.

练习册系列答案
相关题目
 如图,矩形ABCD的边AB=4,AD=10.点P是BC边上的一个点,如果△ABP与△CDP相似,那么符合条件的点P有
如图,矩形ABCD的边AB=4,AD=10.点P是BC边上的一个点,如果△ABP与△CDP相似,那么符合条件的点P有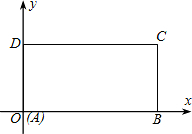 如图,在平面直角坐标系xoy中,已知矩形ABCD的边AB、AD分别在x轴、y轴上,点A与坐标原点重合,且AB=2,AD=1.
如图,在平面直角坐标系xoy中,已知矩形ABCD的边AB、AD分别在x轴、y轴上,点A与坐标原点重合,且AB=2,AD=1. (2012•怀柔区二模)如图,矩形ABCD的边AB=5cm,BC=4cm动点P从A点出发,在折线AD-DC-CB上以1cm/s 的速度向B点作匀速运动,则表示△ABP的面积S(cm)与运动时间t(s)之间的函数系的图象是( )
(2012•怀柔区二模)如图,矩形ABCD的边AB=5cm,BC=4cm动点P从A点出发,在折线AD-DC-CB上以1cm/s 的速度向B点作匀速运动,则表示△ABP的面积S(cm)与运动时间t(s)之间的函数系的图象是( ) 如图,矩形ABCD的边AB在y轴上,AB的中点与原点重合,AB=2,AD=1,过定点Q(3,0)和动点P(0,a)的直线与矩形ABCD的边有公共点,则a的取值范围是( )
如图,矩形ABCD的边AB在y轴上,AB的中点与原点重合,AB=2,AD=1,过定点Q(3,0)和动点P(0,a)的直线与矩形ABCD的边有公共点,则a的取值范围是( )