题目内容
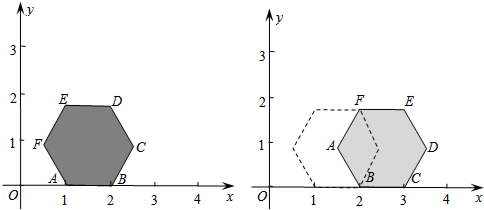
如图,在平面直角坐标系xOy中,点A(1,0),B(2,0),正六边形ABCDEF沿x轴正方向无滑动滚动,当点D第一次落在x轴上时,点D的坐标为: ;在运动过程中,点A的纵坐标的最大值是 ;保持上述运动过程,经过(2014,
)的正六边形的顶点是 .
| 3 |

考点:正多边形和圆,规律型:点的坐标
专题:
分析:利用正多边形的性质以及点的坐标性质,即可得出D点坐标,进而连接A′D,过点F′,E′作F′G⊥A′D,E′H⊥A′D,由正六边形的性质得出A′的坐标,再根据每6个单位长度正好等于正六边形滚动一周即可得出结论.
解答: 解:∵点A(1,0),B(2,0),
解:∵点A(1,0),B(2,0),
∴OA=1,OB=2,
∴正六边形的边长为:AB=1,
∴当点D第一次落在x轴上时,OD=2+1+1=4,
∴此时点D的坐标为:(4,0);
如图1所示:
当滚动到A′D⊥x轴时,E、F、A的对应点分别是E′、F′、A′,连接A′D,点F′,E′作F′G⊥A′D,E′H⊥A′D,
∵六边形ABCDEF是正六边形,
∴∠A′F′G=30°,
∴A′G=
A′F′=
,
同理可得:HD=
,
∴A′D=2,
 ∴在运动过程中,点A的纵坐标的最大值是:2;
∴在运动过程中,点A的纵坐标的最大值是:2;
如图1,∵D(2,0)
∴A′(2,2),OD=2,
∵正六边形滚动6个单位长度时正好滚动一周,
∴从点(2,2)开始到点(2014,
)正好滚动2012个单位长度,
∵
=335…2,
∴恰好滚动335周多2个,如图2所示,F′点纵坐标为:
,
∴会过点(2014,
)的是点F,
当点D还是在(2014,0)位置,
则E点在(2015,0)位置,此时B点在D点的正上方,DB=
,所以B点符合题意.
故答案为:(4,0),2,F或B.
 解:∵点A(1,0),B(2,0),
解:∵点A(1,0),B(2,0),∴OA=1,OB=2,
∴正六边形的边长为:AB=1,
∴当点D第一次落在x轴上时,OD=2+1+1=4,
∴此时点D的坐标为:(4,0);
如图1所示:
当滚动到A′D⊥x轴时,E、F、A的对应点分别是E′、F′、A′,连接A′D,点F′,E′作F′G⊥A′D,E′H⊥A′D,
∵六边形ABCDEF是正六边形,
∴∠A′F′G=30°,
∴A′G=
| 1 |
| 2 |
| 1 |
| 2 |
同理可得:HD=
| 1 |
| 2 |
∴A′D=2,
 ∴在运动过程中,点A的纵坐标的最大值是:2;
∴在运动过程中,点A的纵坐标的最大值是:2;如图1,∵D(2,0)
∴A′(2,2),OD=2,
∵正六边形滚动6个单位长度时正好滚动一周,
∴从点(2,2)开始到点(2014,
| 3 |
∵
| 2012 |
| 6 |
∴恰好滚动335周多2个,如图2所示,F′点纵坐标为:
| 3 |
∴会过点(2014,
| 3 |
当点D还是在(2014,0)位置,
则E点在(2015,0)位置,此时B点在D点的正上方,DB=
| 3 |
故答案为:(4,0),2,F或B.
点评:本题考查的是正多边形和圆及图形旋转的性质,根据题意作出辅助线,利用正六边形的性质求出A′点的坐标是解答此题的关键.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
| 3 | -27 |
| A、-3 | ||
| B、3 | ||
C、
| ||
D、-
|
下列说法正确的是( )
| A、0的平方根是0 | ||||
| B、9的立方根是3 | ||||
C、
| ||||
D、
|
 =0,
=0, =-5,
=-5, =12,
=12, =
= 如图,在菱形ABCD中,AC、BD相交于点O,E为AB的中点,若OE=2,则菱形ABCD的周长是
如图,在菱形ABCD中,AC、BD相交于点O,E为AB的中点,若OE=2,则菱形ABCD的周长是 如图,⊙O的两条弦AB、CD相交于点P,∠D=30°,∠APD=80°,则∠C=
如图,⊙O的两条弦AB、CD相交于点P,∠D=30°,∠APD=80°,则∠C=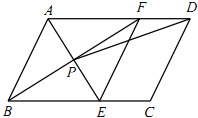 如图,在?ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.
如图,在?ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.