Question

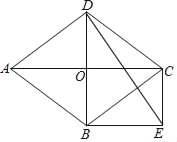
【题目】如图，在菱形ABCD中，对角线AC和BD交于点O，分别过点B、C作BE∥AC，CE∥BD，BE与CE交于点E．

（1）求证：四边形OBEC是矩形；

（2）当∠ABD=60°，AD=2时，求∠EDB的正切值．

Answer 1

【答案】（1）证明见解析；（2）

【解析】分析：（1）先依据平行四边形的定义证明四边形OBEC为平行四边形，然后再依据矩形的性质得到∠COB=90°，故此四边形OBEC是矩形；

（2）依据有一个角为60°的等腰三角形是等边三角形可得到BD=2，然后利用特殊锐角三角函数值可求得AO的长，从而得到BE的长，最后利用锐角三角函数的定义求解即可．

详解：（1）∵BE∥AC，CE∥BD，∴四边形OBEC为平行四边形．

∵ABCD为菱形，∴AC⊥BD，∴∠BOC=90°，∴四边形OBEC是矩形．

（2）∵AD=AB，∠DAB=60°，∴△ABD为等边三角形，∴BD=AD=AB=2．

∵ABCD为菱形，∠DAB=60°，∴∠BAO=30°，∴OC=OA=3，∴BE=3，

∴tan∠EDB===．