题目内容
 如图,直线l1∥l2,AB⊥l1于O,BC交l2于点E.
如图,直线l1∥l2,AB⊥l1于O,BC交l2于点E.
(1)若∠1=20°,求∠2的度数.
(2)若∠1=n°,求∠2的度数.
(3)通过求(1)、(2)两问中∠2的度数,你发现∠1与∠2的度数有什么关系?
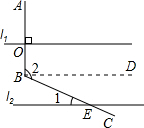 解:如图,过点B作BD∥直线l1.
解:如图,过点B作BD∥直线l1.∵AB⊥l1,
∴AB⊥BD,即∠ABD=90°,
∵直线l1∥l2,
∴∠DBC=∠1,
∴∠2=∠ABD+∠DBC=90°+∠1;
(1)若∠1=20°时,∠2=90°+20°=110°;
(2)若∠1=n°时,∠2=90°+n°;
(3)∠2-∠1=90°,即∠2与∠1的差的定值90°.
分析:(1)、(2)如图,过点B作BD∥直线l1,则根据平行线的性质知∠ABD=90°,∠DBC=∠1,则∠2=∠ABD+∠DBC;
(3)利用(2)的结论可以得到∠2-∠1=90°.
点评:本题考查了平行线的性质.平行线性质定理
定理1:两条平行线被第三条直线所截,同位角相等. 简单说成:两直线平行,同位角相等.
定理2:两条平行线被地三条直线所截,同旁内角互补..简单说成:两直线平行,同旁内角互补.
定理3:两条平行线被第三条直线所截,内错角相等. 简单说成:两直线平行,内错角相等.

练习册系列答案
相关题目
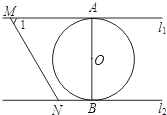 如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B.点M和点N分别是l1和l2上的动点,MN沿l1和l2平移.⊙O的半径为1,∠1=60°.下列结论错误的是( )
如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B.点M和点N分别是l1和l2上的动点,MN沿l1和l2平移.⊙O的半径为1,∠1=60°.下列结论错误的是( )A、MN=
| ||||
B、若MN与⊙O相切,则AM=
| ||||
| C、若∠MON=90°,则MN与⊙O相切 | ||||
| D、l1和l2的距离为2 |
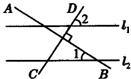 23、如图,直线L1∥L2,AB⊥CD,∠1=34°,那么∠2的度数是
23、如图,直线L1∥L2,AB⊥CD,∠1=34°,那么∠2的度数是 如图,直线l1∥l2,AF:FB=2:3,BC:CD=2:1,则AE:EC是
如图,直线l1∥l2,AF:FB=2:3,BC:CD=2:1,则AE:EC是 14、如图,直线l1∥l2,∠1=55°,∠2=65°,则∠3=
14、如图,直线l1∥l2,∠1=55°,∠2=65°,则∠3= (2009•无锡二模)如图,直线L1∥L2,AB⊥CD,∠1=34°,那么∠2的度数是
(2009•无锡二模)如图,直线L1∥L2,AB⊥CD,∠1=34°,那么∠2的度数是