题目内容
【题目】已知
，
分别是四边形
和
的对角线，点
在
内，
.
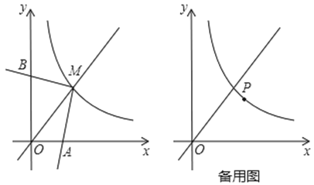
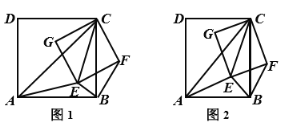
（1）如图1，当四边形和均为正方形时，连接
.
①求证：
∽
；
②若
，
，求
的长；
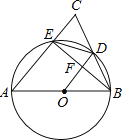
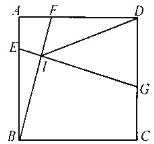
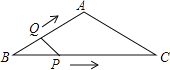
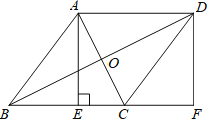
（2）如图2，当四边形和均为矩形，且
时，若，，
，求
的值；
【答案】（1）①证明见解析，②
；（2）
.
【解析】
（1）①由正方形的性质可知
，
，结合题中所给条件可知
，根据两边对应成比例且夹角相等的两个三角形相似可证
∽
；②由相似的性质可得
，
，可求出BF长及
，由勾股定理得
，再次用勾股定理可得CE的长；
（2）设
，则
，设
，则
，由勾股定理得
，可证得
∽
，由相似的性质知
，，求出BF长，易证，再次利用勾股定理用含k的式子表示出EF长，由
可得k值.
（1）①证明：∵四边形
和
均为正方形
∴
，
∴
∴∽
②解：∵∽
∴，
又∵
，
∴
又∵
∴
∴
∴
∴
∴
∴
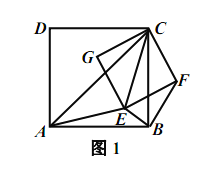
（2）如图，∵四边形和均为矩形
∵
，设，则，设，则
∴
∴
又
∴∽
∴，
又∵
∴
∵，
∴
∴
∴
∵
，
∴
∴
∴
练习册系列答案
相关题目
