题目内容
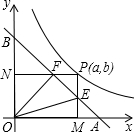 如图,已知直角坐标系内有一条直线和一条曲线,这条直线和x轴、y轴分别交于点A和点B,且OA=OB=1.这条曲线是函数y=
如图,已知直角坐标系内有一条直线和一条曲线,这条直线和x轴、y轴分别交于点A和点B,且OA=OB=1.这条曲线是函数y=| 1 | 2x |
分析:根据OA=OB,得到△AOB是等腰直角三角形,则△NBF也是等腰直角三角形,由于P的纵坐标是b,因而F点的纵坐标是b,即FM=b,则得到AF=
b,同理BE=
a,根据(a,b)是函数y=
的图象上的点,因而b=
,ab=
,则即可求出AF•BE.
| 2 |
| 2 |
| 1 |
| 2x |
| 1 |
| 2a |
| 1 |
| 2 |
解答:解:∵P的坐标为(a,
),且PN⊥OB,PM⊥OA,
∴N的坐标为(0,
),M点的坐标为(a,0),
∴BN=1-
,
在直角三角形BNF中,∠NBF=45°(OB=OA=1,三角形OAB是等腰直角三角形),
∴NF=BN=1-
,
∴F点的坐标为(1-
,
),
∵OM=a,
∴AM=1-a,
∴EM=AM=1-a,
∴E点的坐标为(a,1-a),
∴AF2=(-
)2+(
)2=
,BE2=(a)2+(-a)2=2a2,
∴AF•BE=1.
故答案为:1.
| 1 |
| 2a |
∴N的坐标为(0,
| 1 |
| 2a |
∴BN=1-
| 1 |
| 2a |
在直角三角形BNF中,∠NBF=45°(OB=OA=1,三角形OAB是等腰直角三角形),
∴NF=BN=1-
| 1 |
| 2a |
∴F点的坐标为(1-
| 1 |
| 2a |
| 1 |
| 2a |
∵OM=a,
∴AM=1-a,
∴EM=AM=1-a,
∴E点的坐标为(a,1-a),
∴AF2=(-
| 1 |
| 2a |
| 1 |
| 2a |
| 1 |
| 2a2 |
∴AF•BE=1.
故答案为:1.
点评:本题主要考查了反比例函数图象上的点的特点,图象上所有的点都满足函数解析式.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
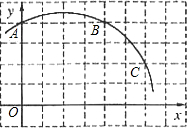 如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.
如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C. 12、如图,已知直角坐标系中的点A、B的坐标分别为A(2,4)、B(4,0),且P为AB的中点.若将线段AB向右平移3个单位后,与点P对应的点为Q,则点Q的坐标是( )
12、如图,已知直角坐标系中的点A、B的坐标分别为A(2,4)、B(4,0),且P为AB的中点.若将线段AB向右平移3个单位后,与点P对应的点为Q,则点Q的坐标是( ) 7、如图,已知直角坐标系中一条圆弧经过正方形网格的格点A,B,C.若A点的坐标为(0,4),D点的坐标为(7,0),那么圆心M点的坐标( )
7、如图,已知直角坐标系中一条圆弧经过正方形网格的格点A,B,C.若A点的坐标为(0,4),D点的坐标为(7,0),那么圆心M点的坐标( )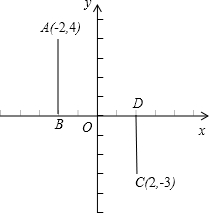 如图,已知直角坐标系中四点A(-2,4),B(-2,0),C(2,-3),D(2,0)、设P是x轴上的点,且PA、PB、AB所围成的三角形与PC、PD、CD所围成的三角形相似,请写出所有符合上述条件的点P的坐标:
如图,已知直角坐标系中四点A(-2,4),B(-2,0),C(2,-3),D(2,0)、设P是x轴上的点,且PA、PB、AB所围成的三角形与PC、PD、CD所围成的三角形相似,请写出所有符合上述条件的点P的坐标: 如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.用直尺和圆规画出该圆弧所在圆的圆心M的位置(不用写作法,保留作图痕迹).
如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.用直尺和圆规画出该圆弧所在圆的圆心M的位置(不用写作法,保留作图痕迹).