题目内容
【题目】如图1,四边形![]() 的对角线
的对角线![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() .
.
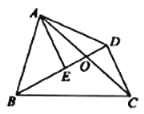
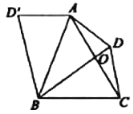
图1 图2
(1)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
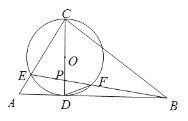
(2)如图2,将![]() 沿
沿![]() 翻折得到
翻折得到![]() .
.
①求证:![]() ;
;
②若![]() ,求证:
,求证:![]() .
.
【答案】(1)见解析;(2)①见解析;②见解析.
【解析】
(1)连接CE,根据全等证得AE=CD,进而AECD为平行四边形,由![]() 进行等边代换,即可得到
进行等边代换,即可得到![]() ;
;
(2)①过A作AE∥CD交BD于E,交BC于F,连接CE,![]() ,得
,得![]() ,利用翻折的性质得到
,利用翻折的性质得到![]() ,即可证明;②证△BEF≌△CDE,从而得
,即可证明;②证△BEF≌△CDE,从而得![]() ,进而得∠CED=∠BCD,且
,进而得∠CED=∠BCD,且![]() ,得到△BCD∽△CDE,得
,得到△BCD∽△CDE,得![]() ,即可证明.
,即可证明.
解:(1)连接CE,
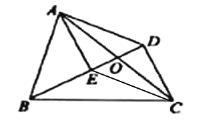
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴△OAE≌△OCD,
∴AE=CD,
∴四边形AECD为平行四边形,
∴AE=CD,OE=OD,
∵![]() ,
,
∴CD=BE,
∴![]() ;
;
(2)①过A作AE∥CD交BD于E,交BC于F,连接CE,
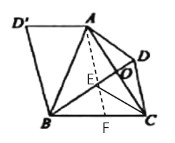
由(1)得,![]() ,
,
∴![]() ,
,
由翻折的性质得![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
②∵![]() ,
,![]() ,
,
∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴EF=DE,
∵四边形AECD是平行四边形,
∴CD=AE=BE,
∵AF∥CD,
∴![]() ,
,
∵EF=DE,CD=BE,![]() ,
,
∴△BEF≌△CDE(SAS),
∴![]() ,
,
∵![]() ,
,
∴∠CED=∠BCD,
又∵∠BDC=∠CDE,
∴△BCD∽△CDE,
∴![]() ,即
,即![]() ,
,
∵DE=2OD,
∴![]() .
.

 阅读快车系列答案
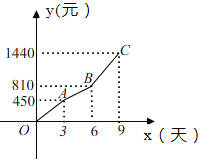
阅读快车系列答案【题目】为了解甲、乙两种车的刹车距离,经试验发现,甲车的刹车距离s甲是车速v的![]() ,乙车的刹车距离s乙等于反应距离与制动距离之和,二反应距离与车速v成正比,制动距离与车速v2成正比,具体关系如下表:
,乙车的刹车距离s乙等于反应距离与制动距离之和,二反应距离与车速v成正比,制动距离与车速v2成正比,具体关系如下表:
车速v(km/h) | 40 | 50 |
刹车距离s乙(m) | 12 | 17.5 |
(1)分别求出s甲、s乙与车速v的函数关系式;
(2)若乙车在限速120km/h的高速公路上行驶,乙车的最长刹车距离是多少m?
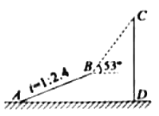
(3)刹车速度是处理交通事故的一个重要因素,请看下面一个交通事故案例:甲、乙两车在限速为80km/g的道路上相向而行,等望见对方,同时刹车时已晚,两车还是相撞了,事后经现场勘查,测得甲车的刹车距离超过16m,但小于18m,乙车的刹车距离是24m,请你比较两车的速度,并判断哪辆车超速?
【题目】为了了解学生关注热点新闻的情况,“两会”期间,小明对班级同学一周内收看“两会”新闻的次数情况作了调查,调查结果统计如图所示(其中男生收看![]() 次的人数没有标出).
次的人数没有标出).
根据上述信息,解答下列各题:
 ×
×
(1)该班级女生人数是__________,女生收看“两会”新闻次数的中位数是________;
(2)对于某个群体,我们把一周内收看某热点新闻次数不低于![]() 次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低
次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低![]() ,试求该班级男生人数;
,试求该班级男生人数;
(3)为进一步分析该班级男、女生收看“两会”新闻次数的特点,小明给出了男生的部分统计量(如表).
统计量 | 平均数(次) | 中位数(次) | 众数(次) | 方差 | … |
该班级男生 |
|
|
|
| … |
根据你所学过的统计知识,适当计算女生的有关统计量,进而比较该班级男、女生收看“两会”新闻次数的波动大小.