题目内容
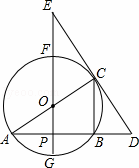
如图所示,△ABC内接于⊙O,AB是⊙O的直径,D是AB延长线上一点,连接DC,且AC=DC,BC=BD.
(1)求证:DC是⊙O的切线;
(2)作CD的平行线AE交⊙O于点E,已知DC=10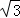 ,求圆心O到AE的距离.
,求圆心O到AE的距离.
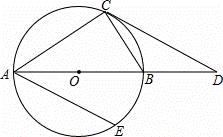
(1)证明:连接OC,
∵AC=DC,BC=BD,
∴∠CAD=∠D,∠D=∠BCD,
∴∠CAD=∠D=∠BCD,
∴∠ABC=∠D+∠BCD=2∠CAD,
设∠CAD=x°,则∠D=∠BCD=x°,∠ABC=2x°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴x+2x=90,
x=30,
即∠CAD=∠D=30°,∠CBO=60°,
∵OC=OB,
∴△BCO是等边三角形,
∴∠COB=60°,
∴∠OCD=180°﹣30°﹣60°=90°,
即OC⊥CD,
∵OC为半径,
∴DC是⊙O的切线;
(2)解:过O作OF⊥AE于F,
∵在Rt△OCD中,∠OCD=90°,∠D=30°,CD=10 ,
,
∴OC=CD×tan30°=10,
OD=2OC=20,
∴OA=OC=10,
∵AE∥CD,
∴∠FAO=∠D=30°,
∴OF=AO×sin30°=10×=5,
即圆心O到AE的距离是5.



如图,直角坐标系中的五角星关于y轴对称的图形在( )

|
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
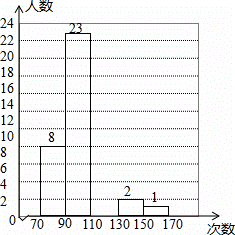
某校为了了解学生大课间活动的跳绳情况,随机抽取了50名学生每分钟跳绳的次数进行统计,把统计结果绘制成如表和直方图.
| 次数 | 70<x<90 | 90<x<110 | 110≤x<130 | 130≤x<150 | 150≤x<170 |
| 人数 | 8 | 23 | 16 | 2 | 1 |
根据所给信息,回答下列问题:
(1)本次调查的样本容量是 ;
(2)本次调查中每分钟跳绳次数达到110次以上(含110次)的共有的共有 人;
(3)根据上表的数据补全直方图;
(4)如果跳绳次数达到130次以上的3人中有2名女生和一名男生,学校从这3人中抽取2名学生进行经验交流,求恰好抽中一男一女的概率(要求用列表法或树状图写出分析过程).
PM2.5是指大气中直径小于或等于0.000 002 5米的颗粒物,将0.000 002 5用科学记数法表示为( )
|
| A. | 0.25×10﹣5 | B. | 2.5×10﹣5 | C. | 2.5×10﹣6 | D. | 2.5×10﹣7 |
 ﹣|﹣3
﹣|﹣3 |
| ×
× =
=  ABC外接圆半径为R,且2R(
ABC外接圆半径为R,且2R( )=
)= ,则角C=( )
,则角C=( ) .
. ,求DE的长.
,求DE的长.