题目内容
已知矩形纸片ABCD中,AB=2,BC=3.
操作:将矩形纸片沿EF折叠,使点B落在边CD上.
探究:
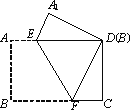
(1)如下图,若点B与点D重合,你认为△EDA1和△FDC全等吗?如果全等给出证明,如果不全等请说明理由;
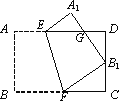
(2)如下图,若点B与CD的中点重合,求△FCB1和△B1DG的周长之比.
答案:
解析:
解析:
|
解:(1)全等 证明:∵四边形ABCD是矩形 ∴∠A=∠B=∠C=∠ADC=90°,AB=CD 由题意知:∠A=∠ ∴∠ ∴∠ ∴△ED (2)∵∠DGB1+∠DB1G=90°,∠DB1G+∠CB1F=90° ∴∠DGB1=∠CB1F ∵∠D=∠C=90° ∴△FCB1∽△B1DG 设FC= ∴ ∴ ∵△FCB1∽△B1DG ∴ |

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目

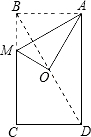 如图,已知矩形纸片ABCD中,AD=6,AB=a(a<6),在BC边上取一点M,将△ABM沿AM折叠后点B恰好落在矩形ABCD的对称中心O处,则a的值为
如图,已知矩形纸片ABCD中,AD=6,AB=a(a<6),在BC边上取一点M,将△ABM沿AM折叠后点B恰好落在矩形ABCD的对称中心O处,则a的值为