题目内容
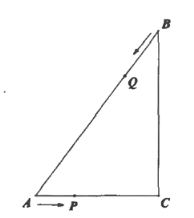
【题目】如图,已知![]() 中,
中,![]() ,点
,点![]() 以每秒1个单位的速度从
以每秒1个单位的速度从![]() 向
向![]() 运动,同时点
运动,同时点![]() 以每秒2个单位的速度从
以每秒2个单位的速度从![]() 向
向![]() 方向运动,
方向运动,![]() 到达
到达![]() 点后,
点后,![]() 点也停止运动,设点
点也停止运动,设点![]() 运动的时间为
运动的时间为![]() 秒.
秒.
(1)求![]() 点停止运动时,
点停止运动时,![]() 的长;
的长;
(2) ![]() 两点在运动过程中,点
两点在运动过程中,点![]() 是
是![]() 点关于直线
点关于直线![]() 的对称点,是否存在时间
的对称点,是否存在时间![]() ,使四边形
,使四边形![]() 为菱形?若存在,求出此时
为菱形?若存在,求出此时![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3) ![]() 两点在运动过程中,求使
两点在运动过程中,求使![]() 与
与![]() 相似的时间
相似的时间![]() 的值.
的值.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() 或
或![]()
【解析】
(1)求出点Q的从B到A的运动时间,再求出AP的长,利用勾股定理即可解决问题.
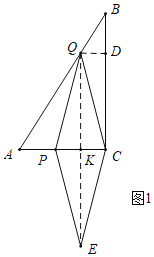
(2)如图1中,当四边形PQCE是菱形时,连接QE交AC于K,作QD⊥BC于D.根据DQ=CK,构建方程即可解决问题.
(3)分两种情形:如图3-1中,当∠APQ=90°时,如图3-2中,当∠AQP=90°时,分别构建方程即可解决问题.
(1)在Rt△ABC中,∵∠C=90°,AC=6,BC=8,
∴AB=![]() =10,
=10,
点Q运动到点A时,t=![]() =5,
=5,
∴AP=5,PC=1,
在Rt△PBC中,PB=![]() .
.
(2)如图1中,当四边形PQCE是菱形时,连接QE交AC于K,作QD⊥BC于D.
∵四边形PQCE是菱形,
∴PC⊥EQ,PK=KC,
∵∠QKC=∠QDC=∠DCK=90°,
∴四边形QDCK是矩形,
∴DQ=CK,
∴![]() ,
,
解得t=![]() .
.
∴t=![]() s时,四边形PQCE是菱形.
s时,四边形PQCE是菱形.
(3)如图2中,当∠APQ=90°时,
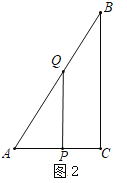
∵∠APQ=∠C=90°,
∴PQ∥BC,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
如图3中,当∠AQP=90°时,

∵△AQP∽△ACB,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
综上所述,![]() 或
或![]() s时,△APQ是直角三角形.
s时,△APQ是直角三角形.

【题目】阅读下列材料:
有这样一个问题:关于x 的一元二次方程a x2+bx+c=0(a>0)有两个不相等的且非零的实数根.探究a,b,c满足的条件.
小明根据学习函数的经验,认为可以从二次函数的角度看一元二次方程,下面是小明的探究过程:
①设一元二次方程ax2+bx+c=0(a>0)对应的二次函数为y=ax2+bx+c(a>0);
②借助二次函数图象,可以得到相应的一元二次中a,b,c满足的条件,列表如下:
方程根的几何意义:请将(2)补充完整
方程两根的情况 | 对应的二次函数的大致图象 | a,b,c满足的条件 |
方程有两个 不相等的负实根 |
|
|
_____ |
|
|
方程有两个 不相等的正实根 | _____ | _____ |
(1)参考小明的做法,把上述表格补充完整;
(2)若一元二次方程mx2﹣(2m+3)x﹣4m=0有一个负实根,一个正实根,且负实根大于﹣1,求实数m的取值范围.