题目内容
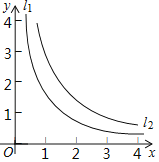
【题目】点A是反比例函数y=![]() (x>0)的图象l1上一点,直线AB∥x轴,交反比例函数y=
(x>0)的图象l1上一点,直线AB∥x轴,交反比例函数y=![]() (x>0)的图象l2于点B,直线AC∥y轴,交l2于点C,直线CD∥x轴,交l1于点D.
(x>0)的图象l2于点B,直线AC∥y轴,交l2于点C,直线CD∥x轴,交l1于点D.
(1)若点A(1,1),求线段AB和CD的长度;
(2)对于任意的点A(a,b),判断线段AB和CD的大小关系,并证明.
【答案】(1)AB=2,CD=![]() ;(2)AB>CD,证明详见解析.
;(2)AB>CD,证明详见解析.
【解析】
(1)根据题意求得B(3,1),C(1,3),D(![]() ,3),即可求得AB和CD 长度;
,3),即可求得AB和CD 长度;
(2)根据题意得到A(a,![]() ),B(3a,
),B(3a,![]() ).C(a,
).C(a,![]() ),D(
),D(![]() ,
,![]() ),进一步求得AB=2a,CD=
),进一步求得AB=2a,CD=![]() .即可求得AB>CD.
.即可求得AB>CD.
解:(1)∵AB∥x轴,A(1,1),B在反比例函数![]() 的图象上,
的图象上,
∴B(3,1).
同理可求:C(1,3),D(![]() ,3).
,3).
∴AB=2,CD=![]() .
.
(2)AB>CD.
证明:∵A(a,b),A在反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴A(a,![]() ).
).
∵AB∥x轴,B在反比例函数![]() 的图象上,
的图象上,
∴B(3a,![]() ).
).
同理可求:C(a,![]() ),D(
),D(![]() ,
,![]() ).
).
∴AB=2a,CD=![]() .
.
∵a>0,
∴2a>![]() .
.
∴AB>CD.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某超市为了销售一种新型“吸水拖把”,对销售情况作了调查,结果发现每月销售量y(只)与销售单价x(元)满足一次函数关系,所调查的部分数据如表:(已知每只进价为10元,销售单价为整数,每只利润=销售单价﹣进价)
销售单价x(元) | 20 | 22 | 25 | … |
月销售额y(只) | 300 | 280 | 250 | … |
(1)求出y与x之间的函数表达式
(2)该新型“吸水拖把”每月的总利润为w(元),求w关于x的函数表达式,并指出销售单价为多少元时利润最大,最大利润是多少元?