题目内容
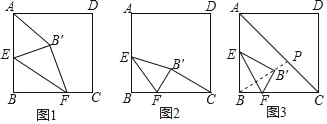
【题目】正方形ABCD的边长是10，点E是AB的中点，动点F在边BC上，且不与点B、C重合，将△EBF沿EF折叠，得到△EB′F．
（1）如图1，连接AB′．
①若△AEB′为等边三角形，则∠BEF等于多少度．
②在运动过程中，线段AB′与EF有何位置关系？请证明你的结论．
（2）如图2，连接CB′，求△CB′F周长的最小值．
（3）如图3，连接并延长BB′，交AC于点P，当BB′＝6时，求PB′的长度．
【答案】（1）①∠BEF＝60°；②A B'∥EF，证明见解析；（2）△CB′F周长的最小值5+5
；（3）PB′＝
．
【解析】
（1）①当△AEB′为等边三角形时，∠AE B′＝60°，由折叠可得，∠BEF＝ 
∠BE B′＝ ×120°＝60°；②依据AE＝B′E，可得∠EA B′＝∠E B′A，再根据∠BEF＝∠B′EF，即可得到∠BEF＝∠BA B′，进而得出EF∥A B′；
（2）由折叠可得，CF+ B′F＝CF+BF＝BC＝10，依据B′E+ B′C≥CE，可得B′C≥CE﹣B′E＝5﹣5，进而得到B′C最小值为5﹣5，故△CB′F周长的最小值＝10+5﹣5＝5+5；
（3）将△ABB′和△APB′分别沿AB、AC翻折到△ABM和△APN处，延长MB、NP相交于点Q，由∠MAN＝2∠BAC＝90°，∠M＝∠N＝90°，AM＝AN，可得四边形AMQN为正方形，设PB′＝PN＝x，则BP＝6+x，BQ＝8﹣6＝2，QP＝8﹣x．依据∠BQP＝90°，可得方程22+（8﹣x）2＝（6+x）2，即可得出PB′的长度．
（1）①当△AE B′为等边三角形时，∠AE B′＝60°，
由折叠可得，∠BEF＝∠BE B′＝×120°＝60°，
故答案为：60；
②A B′∥EF，
证明：∵点E是AB的中点，
∴AE＝BE，
由折叠可得BE＝B′E，
∴AE＝B′E，
∴∠EA B′＝∠E B′A，
又∵∠BEF＝∠B′EF，
∴∠BEF＝∠BA B′，
∴EF∥A B′；
（2）如图，点B′的轨迹为半圆，由折叠可得，BF＝B′F，
∴CF+ B′F＝CF+BF＝BC＝10，
∵B′E+ B′C≥CE，
∴B′C≥CE﹣B′E＝5﹣5，
∴B′C最小值为5﹣5，
∴△CB′F周长的最小值＝10+5﹣5＝5+5；
（3）如图，连接A B′，易得∠A B′B＝90°，
将△AB B′和△AP B′分别沿AB、AC翻折到△ABM和△APN处，延长MB、NP相交于点Q，
由∠MAN＝2∠BAC＝90°，∠M＝∠N＝90°，AM＝AN，可得四边形AMQN为正方形，
由AB＝10，B B′＝6，可得A B′＝8，
∴QM＝QN＝A B′＝8，
设P B′＝PN＝x，则BP＝6+x，BQ＝8﹣6＝2，QP＝8﹣x．
∵∠BQP＝90°，
∴22+（8﹣x）2＝（6+x）2，
解得：x＝，
∴P B′＝x＝．
