题目内容
23、在旧城改造中，要拆除一烟囱AB，承担拆除任务的工人已在地面上划定以B为圆心，半径与AB等长的圆形危险区．现因离B点35米处有一保护文物，为确保文物的安全，文物保护部门决定亲自测定烟囱AB的高度，于是在离B点21米远的建筑物CD顶端C点测得A点的仰角为45°，B点的俯角为30°．问受保护文物是否在危险区内？分析：构造45°所在的直角三角形，那么30°也在直角三角形中．易得AE=CE；利用30°的正切值可求得BE长，加上AE长即为AB长，与35比较即可．
解答：解：做CE⊥AB于点E，
∴∠AEC=∠CEB=90°，
∵∠CDB=∠ABD=90°，
∴四边形CDBE是矩形，
∴BD=CE=21，
∵∠ACE=45°，
∴AE=CE=21，
∵∠BCE=30°，
∴BE=CE×tan30°≈12.12，
∴AB≈33
∴AB＜35，
答：不在危险区．
∴∠AEC=∠CEB=90°，
∵∠CDB=∠ABD=90°，
∴四边形CDBE是矩形，
∴BD=CE=21，
∵∠ACE=45°，
∴AE=CE=21，
∵∠BCE=30°，
∴BE=CE×tan30°≈12.12，
∴AB≈33
∴AB＜35，
答：不在危险区．
点评：构造仰角和俯角所在的直角三角形，利用两个直角三角形的公共边求解是常用的解直角三角形的方法．
练习册系列答案
阅读快车系列答案
相关题目
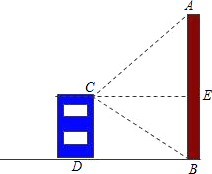在旧城改造中，要拆除一烟囱AB（如图所示），事先应在地面上划定以B为圆心，以AB为半径的圆形危险区，现在从距离B点21米远的建筑物CD顶端C测得A点的仰角为45°，B点的俯角为30°．问离B点35米远的文物是否在危险区内？
我市在旧城改造中，要拆除一个烟囱AB（如图），在烟囱正西方向的楼CD的顶端C处测得烟囱的顶端A的仰角为45°，底端B的俯角为30°，已知DB=21cm．
在旧城改造中，要拆除一个烟囱AB，如图，在地面上事先画出以点B为圆心，半径与AB等长的圆形区域为危险区，BD=21米，在建筑物CD的顶端C点测得点A的仰角为45°，点B的俯角为30°，问距离B点35米远的保护文物是否在危险区内？
在旧城改造中，要拆除一烟囱AB，如图所示，在地面上事先划定以B为圆心，半径与AB等长的圆形危险区，现在从离B点21m的建筑物CD顶端C点测得A点的仰角为45°，B点的俯角为30°，问离B点35m远的保护文物是否在危险区内？（注：从低处观测高处的目标时，视线与水平线所成的锐角称为仰角；而从高处观测低处目标时，视线与水平线所成的锐角称为俯角）