题目内容
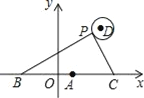
如图，在平面直角坐标系中，已知点A（1，0），B（1﹣a，0），C（1+a，0）（a＞0），点P在以D（4，4）为圆心，1为半径的圆上运动，且始终满足∠BPC=90°，则a的最大值是_______．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
轻巧夺冠周测月考直通中考系列答案题目内容
如图，在平面直角坐标系中，已知点A（1，0），B（1﹣a，0），C（1+a，0）（a＞0），点P在以D（4，4）为圆心，1为半径的圆上运动，且始终满足∠BPC=90°，则a的最大值是_______．
轻巧夺冠周测月考直通中考系列答案
B. 
C. 
D. 
，以点A为圆心，AD为半径的圆与BC相切于点E，交AB于点F.
B. 
C. 
D. 
与
是同类项，则代数式
的值为____.