Question

10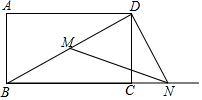．已知，矩形ABCD中，AB=15，AD=20，点M在对角线BD上，点N为射线BC上一动点，连接MN、DN，且∠DNM=∠DBC，当DMN是等腰三角形，线段BN的长是25，40，$\frac{125}{8}$．

Answer 1

分析 分三种情形讨论求解即可．

解答 解：①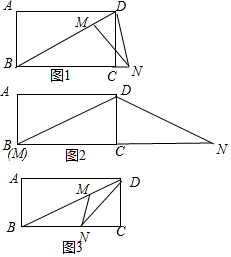如图1中，当NM=ND时，
∴∠NDM=∠NMD，
∵∠MND=∠CBD，
∴∠BDN=∠BND，
∴BD=BN=$\sqrt{B{C}^{2}+C{D}^{2}}$=25．
②如图2中，当DM=DN时，易知M与B重合，此时BC=CN=20，BN=40，
③如图3中，当MN=MD时，易证BN=DN，设BN=DN=x，
在Rt△DNC中，∵DN²=CN²+CD²，
∴x²=（20-x）²+15²，
∴x=$\frac{125}{8}$，
故答案为25，40，$\frac{125}{8}$．

点评 本题考查矩形的性质、等腰三角形的判定和性质、勾股定理等知识，解题的关键是学会用分类讨论的思想思考问题，注意不能漏解．