Question

6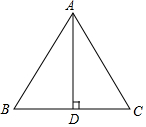．如图，AD是△ABC的边BC上的高，下列条件中不能推出△ABC是等腰三角形的是（　　）

• A． ∠BAD=∠ACD
• B． ∠BAD=∠CAD
• C． AB+BD=AC+CD
• D． AB-BD=AC-CD

Answer 1

分析 可根据等腰三角形三线合一的性质来判断①②是否正确；③④要通过作等腰三角形来判断其结论是否成立．

解答 解：当∠BAD=∠CAD时，
∵AD是∠BAC的平分线，且AD是BC边上的高；
则△ABD≌△ACD，
∴△BAC是等腰三角形；
延长DB至E，使BE=AB；延长DC至F，使CF=AC；连接AE、AF；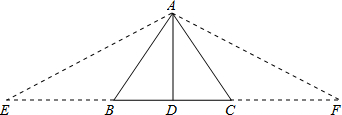

∵AB+BD=CD+AC，
∴DE=DF，又AD⊥BC；
∴△AEF是等腰三角形；
∴∠E=∠F；
∵AB=BE，
∴∠ABC=2∠E；
同理，得∠ACB=2∠F；
∴∠ABC=∠ACB，即AB=AC，△ABC是等腰三角形；
△ABC中，AD⊥BC，根据勾股定理，得：
AB²-BD²=AC²-CD²，
即（AB+BD）（AB-BD）=（AC+CD）（AC-CD）；
∵AB-BD=AC-CD①，
∴AB+BD=AC+CD②；
∴①+②得：，
2AB=2AC；
∴AB=AC，
∴△ABC是等腰三角形
故选A．

点评 此题主要考查的是等腰三角形的判定和性质；本题的难点是结论③的证明，能够正确的构建出等腰三角形是解答③题的关键．