题目内容
【题目】如图,菱形AB1C1D1的边长为1,∠B1=60°;作AD2⊥B1C1于点D2,以AD2为一边,做第二个菱形AB2C2D2,使∠B2=60°;作AD3⊥B2C2于点D3,以AD3为一边做第三个菱形AB3C3D3,使∠B3=60°,依此类推,这样做的第2020个菱形ABnCnDn的边ADn的长是( ).

A.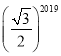 B.
B.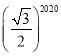 C.
C.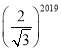 D.
D.
【答案】A
【解析】
在△AB1D2中利用三角函数的定义计算出AD2=![]() ,再根据菱形的性质得AB2=AD2=
,再根据菱形的性质得AB2=AD2=![]() ,则利用三角函数的定义得到AD3=(
,则利用三角函数的定义得到AD3=(![]() )2,同理可得AD4=(
)2,同理可得AD4=(![]() )3,利用此变换规律得到ADn=(
)3,利用此变换规律得到ADn=(![]() )n-1,即可得到答案.
)n-1,即可得到答案.
解:在△AB1D2中,∵sinB1=![]() ,
,
∴AD2=1×sin60°=![]() ,
,
∵四边形AB2C2D2为菱形,
∴AB2=AD2=![]() ,
,
在△AB2D3中,∵sinB2=![]() ,
,
∴AD3=![]() ×sin60°=(
×sin60°=(![]() )2,
)2,
同理可得AD4=(![]() )3,
)3,
∴第n个菱形ABnCnDn的边ADn的长为(![]() )n-1.
)n-1.
∴第2020个菱形ABnCnDn的边ADn的长是![]() ;
;
故选:A.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目