题目内容
【题目】如图，抛物线y=﹣ 
x2+bx+c与x轴交于A，B两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知A（﹣1，0），C（0，2）．
（1）求抛物线的解析式；
（2）在抛物线的对称轴上是否存在点P，使△PCD是以CD为腰的等腰三角形？如果存在，直接写出P点的坐标；如果不存在，请说明理由；
（3）点E时线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，△CBF的面积最大？求出△CBF的最大面积及此时E点的坐标．
【答案】
（1）
解：把A（﹣1，0），C（0，2）代入y=﹣ 
x2+bx+c得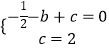 
，
解得 
，c=2，
∴抛物线的解析式为y=﹣ x2+ 
x+2
（2）
解：存在．如图1中，∵C（0，2），D（ ，0），
∴OC=2，OD= ，CD= 
= 
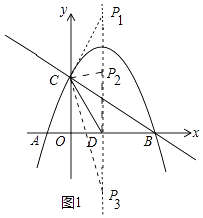
①当CP=CD时，可得P1（ ，4）．
②当DC=DP时，可得P2（ ， ），P3（ ，﹣ ）
综上所述，满足条件的P点的坐标为 
或 
或 
（3）
解：如图2中，
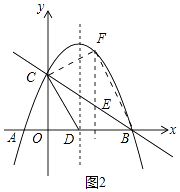
对于抛物线y=﹣ x2+ x+2，当y=0时，﹣ x2+ x+2=0，解得x1=4，x2=﹣1
∴B（4，0），A（﹣1，0），
由B（4，0），C（0，2）得直线BC的解析式为y=﹣ x+2，
设E 
则F 
，
EF= 
﹣ 
= 
∴- ＜0，∴当m=2时，EF有最大值2，
此时E是BC中点，
∴当E运动到BC的中点时，△EBC面积最大，
∴△EBC最大面积= ×4×EF= ×4×2=4，此时E（2，1）
【解析】（1）把A（﹣1，0），C（0，2）代入y=﹣ x2+bx+c列方程组即可．（2）先求出CD的长，分两种情形①当CP=CD时，②当DC=DP时分别求解即可．（3）求出直线BC的解析式，设E 则F ，构建二次函数，利用二次函数的性质即可解决问题．
【考点精析】关于本题考查的二次函数的图象和二次函数的性质，需要了解二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能得出正确答案．
