题目内容
将正方形的四个顶点用线段连接，什么样的连法最短？研究发现，并非对角线最短，而是如图的连法最短(即用线段AE，DE，EF，BF，CF把四个顶点连接起来)．已知图中∠DAE＝∠ADE＝30°，∠AEF＝∠BFE＝120°，你能证明此时AB∥EF吗？
答案：略
解析：
解析：
|
能证明 AB∥EF．理由： ∵四边形ABCD为正方形，∴∠DAE＋∠EAB＝90°．∵∠DAE ＝30°，∴∠EAB＝90°－30°＝60°，∵∠AEF ＝120°，∴∠EAB＋∠AEF＝60°＋120°＝180°．∴AB∥EF ． |
练习册系列答案
相关题目
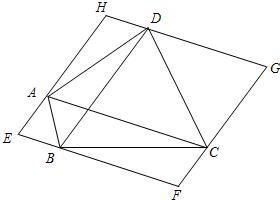
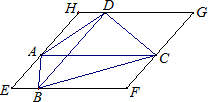24、如图，过四边形ABCD的四个顶点分别作对角线AC、BD的平行线，所围成的四边形EFGH显然是平行四边形．
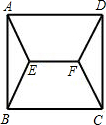ABE=∠FDC=∠FCD=30°，∠AEF=∠DFE且AE=DF．