Question

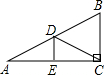已知，如图，△ABC中，∠C=90°，D、E分别是AB、AC的中点，若AC=4，AB=5，则CD=________，DE=________．

Answer 1

    
分析：根据勾股定理易求BC的长．
CD是斜边上的中线，根据直角三角形斜边上的中线等于斜边的一半可得其长度；
DE是中位线，根据中位线定理可求其长度．
解答：∵AC=4，AB=5，∠C=90°，
∴由勾股定理得：BC=3．
∵D、E分别是AB、AC的中点，
∴CD=AB=，
DE=BC=．
故答案为：，．
点评：此题考查的是三角形中位线定理和直角三角形斜边上的中线等于斜边的一半的性质．