题目内容
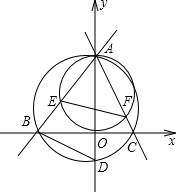 如图直线
如图直线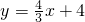 与x轴交于B点,与y轴交于A点,直线y=-2x+b过点A与x轴交于C点.
与x轴交于B点,与y轴交于A点,直线y=-2x+b过点A与x轴交于C点.
(1)求A、B、C三点坐标.
(2)过A、B、C三点作圆交y轴于一点D,再以OA为直径作圆交AB、AC于点E、F.求证:∠AEF=∠ADB.
(3)求EF长.
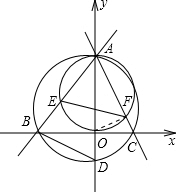 解:连接OF,
解:连接OF,(1)x=0时,y=4
∴A(0.4)
同理B(-3,0),C(2,0)
(2)∵AB是直径,
∴∠AFO=90°,
∴∠AEF=∠AOF=∠ACO,
又∠ACO=∠ADB,
∴∠AEF=∠ADB
(3)由(1)知OA=4,OB=3,OC=2
∴AC=
 =2
=2 ,AB=
,AB= =5
=5∵△AOF∽△ACO
∴

AF=16×
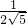 =
=
∵△AEF∽△ACB
∴

∴EF=
 ×
×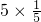
∴EF=

分析:(1)由直线的解析式,分别令x、y为0,可求出点A、B的坐标,由于另一直线过A所以得到b=4,进而得到C的坐标;
(2)连接OF,首先利用AO为直径,利用同角的余角相等,得到∠AOF=∠ACO,然后多次利用同弧所对的圆周角相等,得到多对角相等,进行角的等量代换后可得答案;
(3)首先利用三角形相似,得到相关线段的比例式,求出AF=16×
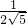 =
= ,再利用△AEF∽△ACB,得到比例式,代入数值可求出EF的长.
,再利用△AEF∽△ACB,得到比例式,代入数值可求出EF的长.点评:本题考查了一次函数的综合应用;在同圆或等圆中,常常用到同弧对的圆周角相等做题,本题第二个问题就多次进行了应用,通过角的等量代换得到答案,是解题的关键,也是下一问解决的前提,注意掌握应用.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
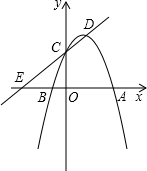 为(3,0).
为(3,0).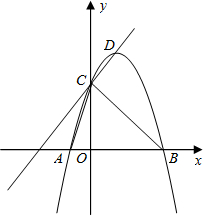 如图,已知二次函数y=-x2+bx+c的图象与x轴交于点A、B,与y轴交于点C,其顶点为D,且直线DC的解析式为y=x+3.
如图,已知二次函数y=-x2+bx+c的图象与x轴交于点A、B,与y轴交于点C,其顶点为D,且直线DC的解析式为y=x+3.
 与x轴交于A,B两点(点B在点A的右侧)与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q。
与x轴交于A,B两点(点B在点A的右侧)与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q。