题目内容
已知如图，E、F在BD上，且AB＝CD，BF＝DE，AE＝CF，求证：AC与EF互相平分。
证明：∵BF=DE，
∴BF-EF=DE-EF
即BE=DF，
在△ABE和△DFC中，
AB="CD" BE="DF" AE=CF ∴△ABE≌△DFC（SSS），
∴∠B=∠D．
在△ABO和△COD中，
∠A0B=∠COD ∠B=∠D AB=CD
∴△ABO≌△COD（AAS），
∴AO=CO，BO=DO，
又∵BE=DF
∴EO=FO
∴AC与EF互相平分解析:
先证△ABE≌△DFC得∠B=∠D，再证△ABO≌△COD，根据全等三角形的性质即可证明AC与EF互相平分
∴BF-EF=DE-EF
即BE=DF，
在△ABE和△DFC中，
AB="CD" BE="DF" AE=CF ∴△ABE≌△DFC（SSS），
∴∠B=∠D．
在△ABO和△COD中，
∠A0B=∠COD ∠B=∠D AB=CD
∴△ABO≌△COD（AAS），
∴AO=CO，BO=DO，
又∵BE=DF
∴EO=FO
∴AC与EF互相平分解析:
先证△ABE≌△DFC得∠B=∠D，再证△ABO≌△COD，根据全等三角形的性质即可证明AC与EF互相平分
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
已知如图，E、F在BD上，且AB=CD，BF=DE，AE=CF，求证：AC与BD互相平分．
36、已知如图，一辆汽车在直线公路AB上由A向B行驶，M，N分别是位于公路AB两侧的村庄．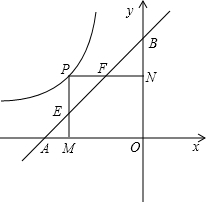
OB=2，PM⊥X轴于M，交AB于点E，PN⊥Y轴于点N，交AB于F；
（x＜0）的图象上运动，点A点B分别在X轴，Y轴上，且OA=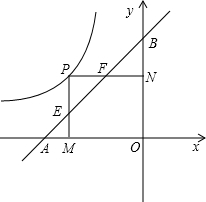
OB=2，PM⊥X轴于M，交AB于点E，PN⊥Y轴于点N，交AB于F；
时，连OE，OF，求E、F两点的坐标及△EOF的面积；
、
、
、
四点在一直线上，
，
∥
，且
．
≌
；
.