题目内容

如图，E为边长为1的正方形ABCD的对角线BD上一点，且BE=BC，P为CE上任意一点，PQ⊥BC，PR⊥BE，则PQ+PR的值为________．

$\text{[math]}$
分析：过E作EF⊥BC于F，由S_△BPC+S_△BPE=S_△BEC推出PQ+PR=EF，在Rt△BEF中求EF．
解答：

解：根据题意，连接BP，过E作EF⊥BC于F，
∵S_△BPC+S_△BPE=S_△BEC
∴ $\text{[math]}$ $\text{[math]}$ = $\text{[math]}$ BC•EF，
∵BE=BC=1，
∴PQ+PR=EF，
∵四边形ABCD是正方形，
∴∠DBC=45°，
∵在Rt△BEF中，∠EBF=45°，BE=1，
sin45°= $\text{[math]}$ ，
∴ $\text{[math]}$ = $\text{[math]}$ ，
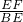∴EF= $\text{[math]}$ ，即PQ+PR= $\text{[math]}$ ．
∴PQ+PR的值为 $\text{[math]}$ ．
故答案为： $\text{[math]}$ ．
点评：解答本题的难点是证明底边上任意一点到等腰三角形两腰的距离等于一腰上的高．在突破难点时，充分利用正方形的性质和三角形面积公式．

练习册系列答案

口算题卡加应用题集训系列答案

中考1加1系列答案

鼎尖阅读系列答案

综合自测系列答案

走进重高培优测试系列答案

中考全程突破系列答案

名师金手指大试卷系列答案

标准课堂测试卷系列答案

智慧翔夺冠金卷系列答案

名校导练系列答案

相关题目

某班甲、乙、丙三位同学进行了一次用正方形纸片折叠探究相关数学问题的课题学习活动．
活动情境：
如图2，将边长为8cm的正方形纸片ABCD沿EG折叠（折痕EG分别与AB、DC交于点E、G），使点B落在AD边上的点 F处，FN与DC交于点M处，连接BF与EG交于点P．
所得结论：
当点F与AD的中点重合时：（如图1）甲、乙、丙三位同学各得到如

下一个正确结论（或结果）：
甲：△AEF的边AE=

cm；
乙：△FDM的周长为16cm；
丙：EG=BF．
你的任务：
（1）填充甲同学所得结果中的数据；
（2）写出在乙同学所得结果的求解过程；
（3）当点F在AD边上除点A、D外的任何一处（如图2）时：
①试问乙同学的结果是否发生变化？请证明你的结论；
②丙同学的结论还成立吗？若不成立，请说明理由，若你认为成立，先证明EG=BF，再求出S（S为四边形AEGD的面积）与x（AF=x）的函数关系式，并问当x为何值时，S最大？最大值是多少？

如图，M是边长为4的正方形AD边的中点，动点P自A点起，由A→B→C→D匀速运动，直线MP扫过正方形所形成的面积为y，点P运动的路程为x，请解答下列问题：

(1)当x＝1时，求y的值；

(2)就下列各种情况，求y与x之间的函数关系式；

①0≤x≤4；②4＜x≤8；③8＜x≤12；

(3)在给出的直角坐标系中，画出(2)中函数的图象．

某班甲、乙、丙三位同学进行了一次用正方形纸片折叠探究相关数学问题的课题学习活动.
活动情境：
如图2，将边长为8cm的正方形纸片ABCD沿EG折叠(折痕EG分别与AB、DC交于点E、G)，使点B落在AD边上的点 F处，FN与DC交于点M处，连接BF与EG交于点P．
所得结论：
当点F与AD的中点重合时：（如图1）甲、乙、丙三位同学各得到如下一个正确结论（或结果）：
甲：△AEF的边AE= cm，EF= cm；
乙：△FDM的周长为16 cm；
丙：EG=BF.
你的任务：
【小题1】填充甲同学所得结果中的数据；
【小题2】写出在乙同学所得结果的求解过程；
【小题3】当点F在AD边上除点A、D外的任何一处（如图2）时：
① 试问乙同学的结果是否发生变化？请证明你的结论；
② 丙同学的结论还成立吗？若不成立，请说明理由，若你认为成立，先证明EG=BF，再求出S（S为四边形AEGD的面积）与x（AF=x）的函数关系式，并问当x为何值时，S最大？最大值是多少？

某班甲、乙、丙三位同学进行了一次用正方形纸片折叠探究相关数学问题的课题学习活动.
活动情境：
如图2，将边长为8cm的正方形纸片ABCD沿EG折叠(折痕EG分别与AB、DC交于点E、G)，使点B落在AD边上的点 F处，FN与DC交于点M处，连接BF与EG交于点P．
所得结论：
当点F与AD的中点重合时：（如图1）甲、乙、丙三位同学各得到如下一个正确结论（或结果）：
甲：△AEF的边AE= cm，EF= cm；
乙：△FDM的周长为16 cm；
丙：EG=BF.
你的任务：
【小题1】填充甲同学所得结果中的数据；
【小题2】写出在乙同学所得结果的求解过程；
【小题3】当点F在AD边上除点A、D外的任何一处（如图2）时：
① 试问乙同学的结果是否发生变化？请证明你的结论；
② 丙同学的结论还成立吗？若不成立，请说明理由，若你认为成立，先证明EG=BF，再求出S（S为四边形AEGD的面积）与x（AF=x）的函数关系式，并问当x为何值时，S最大？最大值是多少？

某班甲、乙、丙三位同学进行了一次用正方形纸片折叠探究相关数学问题的课题学习活动．
活动情境：
如图2，将边长为8cm的正方形纸片ABCD沿EG折叠（折痕EG分别与AB、DC交于点E、G），使点B落在AD边上的点 F处，FN与DC交于点M处，连接BF与EG交于点P．
所得结论：
当点F与AD的中点重合时：（如图1）甲、乙、丙三位同学各得到如下一个正确结论（或结果）：
甲：△AEF的边AE=cm，EF=cm；
乙：△FDM的周长为16cm；
丙：EG=BF．
你的任务：
（1）填充甲同学所得结果中的数据；
（2）写出在乙同学所得结果的求解过程；
（3）当点F在AD边上除点A、D外的任何一处（如图2）时：
①试问乙同学的结果是否发生变化？请证明你的结论；
②丙同学的结论还成立吗？若不成立，请说明理由，若你认为成立，先证明EG=BF，再求出S（S为四边形AEGD的面积）与x（AF=x）的函数关系式，并问当x为何值时，S最大？最大值是多少？