题目内容
在边长为a的正方形中挖掉一个边长为b的小正方形（a＞b）,把余下的部分剪拼成一个矩形（如图），通过计算图形（阴影部分）的面积，验证了一个等式，则这个等式是
- A.a2-b2=(a+b)(a-b)
- B.(a+b)2=a+2ab+b2
- C.(a-b)2=a2-2ab+b2
- D.a2-ab=a(a-b)
A
左图中阴影部分的面积=a2-b2，右图中矩形面积=（a+b）（a-b），根据二者相等，即可求得a2-b2=(a+b)(a-b)
左图中阴影部分的面积=a2-b2，右图中矩形面积=（a+b）（a-b），根据二者相等，即可求得a2-b2=(a+b)(a-b)
练习册系列答案
长江作业本同步练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
相关题目
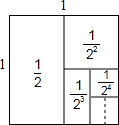在数学兴趣小组活动中，小明为了求
如图，在边长为1的正方形中，以各顶点为圆心，对角线的一半为半径在正方形内作弧，则图中阴影部分的面积是
（如图2），利用这两幅图形面积，可以验证的公式是（ ）