题目内容
如图,二次函数y=- x2+mx+m+
x2+mx+m+ 的图象与x轴相交于点A、B(点A在点B的左
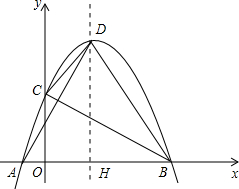
的图象与x轴相交于点A、B(点A在点B的左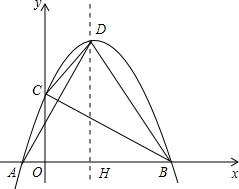 侧),与y轴相交于点C,顶点D在第一象限.过点D作x轴的垂线,垂足为H.
侧),与y轴相交于点C,顶点D在第一象限.过点D作x轴的垂线,垂足为H.
(1)当m= 时,求tan∠ADH的值;
时,求tan∠ADH的值;
(2)当60°≤∠ADB≤90°时,求m的变化范围;
(3)设△BCD和△ABC的面积分别为S1、S2,且满足S1=S2,求点D到直线BC的距离.
 解:(1)∵当m=
解:(1)∵当m= 时,y=-
时,y=- x2+
x2+ x+2=-
x+2=- (x-
(x- )2+
)2+ ,
,∴顶点D(
 ,
, ),与x轴的交点A(-1,0),B(4,0),
),与x轴的交点A(-1,0),B(4,0),∴DH=
 ,AH=
,AH= -(-1)=
-(-1)= ,
,∴tan∠ADH=
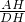 =
=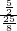 =
= ;
;(2)y=-
 x2+mx+m+
x2+mx+m+ =-
=- (x-m)2+
(x-m)2+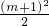 ,
,∴顶点D(m,
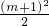 ),
),令y=-
 x2+mx+m+
x2+mx+m+ =0,解得:x=-1或2m+1
=0,解得:x=-1或2m+1则与x轴的交点A(-1,0),B(2m+1,0),
∴DH=
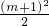 ,AH=m-(-1)=m+1,
,AH=m-(-1)=m+1,∴tan∠ADH=
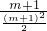 =
= .
.当60°≤∠ADB≤90°时,由对称性得30°≤∠ADH≤45°,
∴当∠ADH=30°时,
 =
= ,
,∴m=2
 -1,
-1,当∠ADH=45°时,
 =1,
=1,∴m=1,
∴1≤m≤2
 -1;
-1;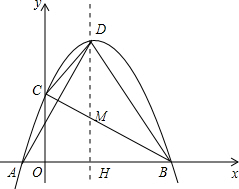 (3)设DH与BC交于点M,则点M的横坐标为m.
(3)设DH与BC交于点M,则点M的横坐标为m.设过点B(2m+1,0),C(0,m+
 )的直线解析式为;y=kx+b,
)的直线解析式为;y=kx+b,则
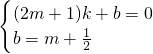 ,
,解得
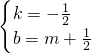 ,
,即y=-
 x+m+
x+m+ .
.当x=m时,y=-
 m+m+
m+m+ =
= ,
,∴M(m,
 ).
).∴DM=
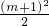 -
- =
=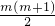 ,AB=(2m+1)-(-1)=2m+2,
,AB=(2m+1)-(-1)=2m+2,又,∵S△DBC=S△ABC,
∴
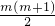 •(2m+1)=(2m+2)•(m+
•(2m+1)=(2m+2)•(m+ ),
),又∵抛物线的顶点D在第一象限,
∴m>0,解得m=2.
当m=2时,A(-1,0),B(5,0),C(0,
 ),
),∴BC=
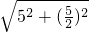 =
= ,
,∴S△ABC=
 ×6×
×6× =
= .
.设点D到直线BC的距离为d.
∵S△DBC=
 BC•d,
BC•d,∴
 ×
× •d=
•d= ,
,∴d=
 .
.答:点D到直线BC的距离为
 .
.分析:(1)先将m=
 代入y=-
代入y=- x2+mx+m+
x2+mx+m+ ,运用配方法改写成顶点式,求出顶点D,与x轴的交点A与B的坐标,得到DH,AH的长度,再根据正切函数的定义即可求出tan∠ADH的值;
,运用配方法改写成顶点式,求出顶点D,与x轴的交点A与B的坐标,得到DH,AH的长度,再根据正切函数的定义即可求出tan∠ADH的值;(2)先将y=-
 x2+mx+m+
x2+mx+m+ 运用配方法改写成顶点式,求出顶点D,与x轴的交点A与B的坐标,得到DH,AH的长度,再由抛物线的对称性可知当60°≤∠ADB≤90°时,30°≤∠ADH≤45°,然后根据30°,45°角的正切函数值及锐角三角函数的增减性即可求出m的变化范围;
运用配方法改写成顶点式,求出顶点D,与x轴的交点A与B的坐标,得到DH,AH的长度,再由抛物线的对称性可知当60°≤∠ADB≤90°时,30°≤∠ADH≤45°,然后根据30°,45°角的正切函数值及锐角三角函数的增减性即可求出m的变化范围;(3)设DH与BC交于点M,则点M的横坐标为m.先运用待定系数法求出直线BC的解析式,则可用含m的代数式表示点M的坐标,再根据S△DBC=S△ABC求出m的值,从而得出A(-1,0),B(5,0),C(0,
 ),S△ABC=
),S△ABC= ×6×
×6× =
= .设点D到直线BC的距离为d,根据S△DBC=
.设点D到直线BC的距离为d,根据S△DBC= BC•d=
BC•d= ,即可求出d的值.
,即可求出d的值.点评:本题是二次函数的综合题型,其中涉及到的知识点有运用待定系数法求函数的解析式,抛物线的顶点坐标公式,正切函数的定义,三角形的面积以及点到直线的距离的求法,综合性较强,有一定难度.其中(3)正确表示S△DBC=
 DM•OB,从而根据S△DBC=S△ABC求出m的值是解题的关键.
DM•OB,从而根据S△DBC=S△ABC求出m的值是解题的关键. 
练习册系列答案
相关题目
 如图,二次函数的图象经过点D(0,
如图,二次函数的图象经过点D(0,
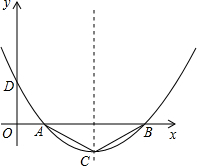
 如图,二次函数y=ax2+bx+c的图象与x轴交于B、C两点,与y轴交于点A(0,-3),∠ABC=45°,∠ACB=60°,求这个二次函数解析式.
如图,二次函数y=ax2+bx+c的图象与x轴交于B、C两点,与y轴交于点A(0,-3),∠ABC=45°,∠ACB=60°,求这个二次函数解析式. 某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,如图的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).根据图象提供的信息,解答下列问题:
某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,如图的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).根据图象提供的信息,解答下列问题: 如图,二次函数y=ax2+bx+c的图象与x轴相交于两个点,根据图象回答:(1)b
如图,二次函数y=ax2+bx+c的图象与x轴相交于两个点,根据图象回答:(1)b