题目内容
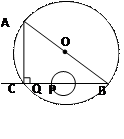
(10分)如图,在Rt△ABC中,∠ACB=90°,AC=6㎝,BC=8㎝,P为BC的中点.动点Q从点P出发,沿射线PC方向以2㎝/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.
⑴求 AB的长;
⑵已知⊙O为△ABC的外接圆,若⊙P与 ⊙O相切,求t的值.
⊙O相切,求t的值.
⑴求 AB的长;
⑵已知⊙O为△ABC的外接圆,若⊙P与
 ⊙O相切,求t的值.
⊙O相切,求t的值.
解(1)在Rt△ABC中,∠ACB=90°,∵AC=6cm,BC=8cm,
∴ . -------------------------------------------------------3分
. -------------------------------------------------------3分
⑵∠ACB=90°,∴AB为△ABC的外切圆的直径.∴ .-----4分
.-----4分
连接OP.∵P为BC的中点,∴ . --------------------------6分
. --------------------------6分
∵点P在⊙O内部,∴⊙P与⊙O只能内切.
∴ 或
或 ,∴
,∴ =1或4.
=1或4.
∴⊙P与⊙O相切时,t的值为1或4.---------------------------------------------------10分
∴
 . -------------------------------------------------------3分
. -------------------------------------------------------3分⑵∠ACB=90°,∴AB为△ABC的外切圆的直径.∴
 .-----4分
.-----4分连接OP.∵P为BC的中点,∴
 . --------------------------6分
. --------------------------6分 ∵点P在⊙O内部,∴⊙P与⊙O只能内切.
∴
 或
或 ,∴
,∴ =1或4.
=1或4. ∴⊙P与⊙O相切时,t的值为1或4.---------------------------------------------------10分
略

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
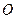 为原点,点
为原点,点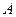 的坐标为
的坐标为 经过
经过 两点作半径为
两点作半径为 的
的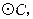 交
交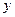 轴的负半轴于点
轴的负半轴于点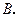

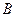 点的坐标;
点的坐标;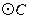 的切线交
的切线交 轴于点
轴于点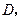 求直线
求直线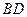 的解析式.
的解析式.
 侧面展开图的圆心角;
侧面展开图的圆心角;
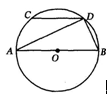
 为
为 的内接三角形,
的内接三角形, 则
则 的扇形围成一个圆锥的侧面,则圆锥的高为 .
的扇形围成一个圆锥的侧面,则圆锥的高为 .