题目内容
如图,点P是菱形ABCD的对角线BD上一点,连结CP并延长,交AD于E,交BA的延长线于点F.试问:
(1) 图中△APD与哪个三角形全等?并说明理由.
(2) 猜想:线段PC、PE、PF之间存在什么关系?并说明理由.
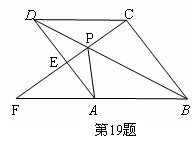 |
解:(1) △APD≌△CPD
理由: ∵四边形ABCD菱形
∴AD=CD, ∠ADP=∠CDP
又∵PD=PD
∴△APD≌△CPD (2) 猜想:
证明:∵△APD≌△CPD
∴∠DAP=∠DCP
∵CD∥BF
∴∠DCP=∠F
∴∠DAP= ∠F
又∵∠APE=∠FPA
∴△APE ∽△FPA
∴ ∴
∴ 
∵△APD≌△CPD
∴PA=PC ∴

练习册系列答案
相关题目


 的侧棱长和底面各边长均为
的侧棱长和底面各边长均为 ,其主视图是边长为
,其主视图是边长为
 B.
B.  C .
C .  D .
D . 
 与
与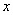 轴、
轴、 轴交于
轴交于 、
、 两点,
两点, 的平分线所在的直线
的平分线所在的直线 的解析式是().
的解析式是(). B.
B. C.
C. D.
D.






 的值以及四边形ABCD的面积.
的值以及四边形ABCD的面积.