题目内容
在△ABC中,若AB=30,AC=26,BC上的高为24,则此三角形的周长为________.
84或64
分析:先根据勾股定理求得BD,CD的长,从而不难求得其周长.
解答: 解:∵在直角三角形ABD中,AB=30,AC=26,AD=24,
解:∵在直角三角形ABD中,AB=30,AC=26,AD=24,
∴DB=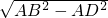 =
= =
= =18;
=18;
∴DC=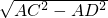 =
= =10;
=10;
当∠ACB是锐角时:BC=DB+DC=18+10=28;
∴三角形的周长=30+26+28=84.
当∠ACB是钝角时:BC=BD-DC=18-10=8.
∴三角形的周长=30+26+8=64.
故三角形的周长为84或64.
点评:勾股定理:在直角三角形中两条直角边的平方和等于斜边的平方.
分析:先根据勾股定理求得BD,CD的长,从而不难求得其周长.
解答:
 解:∵在直角三角形ABD中,AB=30,AC=26,AD=24,
解:∵在直角三角形ABD中,AB=30,AC=26,AD=24,∴DB=
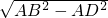 =
= =
= =18;
=18;∴DC=
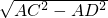 =
= =10;
=10;当∠ACB是锐角时:BC=DB+DC=18+10=28;
∴三角形的周长=30+26+28=84.

当∠ACB是钝角时:BC=BD-DC=18-10=8.
∴三角形的周长=30+26+8=64.
故三角形的周长为84或64.
点评:勾股定理:在直角三角形中两条直角边的平方和等于斜边的平方.

练习册系列答案
相关题目
 9、如图,在△ABC中,若AB=10,AC=16,AC边上的中线BD=6,则BC等于( )
9、如图,在△ABC中,若AB=10,AC=16,AC边上的中线BD=6,则BC等于( ) 如图,△ABC中,点D是BC中点,连接AD并延长到点E,连接BE.
如图,△ABC中,点D是BC中点,连接AD并延长到点E,连接BE. 如图,△ABC中,点D是BC中点,连接AD并延长到点E,连接BE.
如图,△ABC中,点D是BC中点,连接AD并延长到点E,连接BE.