ЬтФПФкШн
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЕФФГдВЩЯЃЌгаЯвMNЃЌШЁMNЕФжаЕуPЃЌЮвУЧЙцЖЈ:ЕуPЕНФГЕуЃЈжБЯпЃЉЕФОрРыНазіЁАЯвжаОрЁБЃЌгУЗћКХЁА![]() ЁББэЪО.
ЁББэЪО.
ЯжЧыдквдWЃЈ-3ЃЌ0ЃЉЮЊдВаФЃЌАыОЖЮЊ2ЕФЁбWдВЩЯЃЌИљОнвдЯТЬѕМўНтД№ЫљЬсЮЪЬтЃК
ЃЈ1ЃЉвбжЊЯвMNГЄЖШЮЊ2.
ЂйШчЭМ1ЃКЕБMNЁЮxжсЪБЃЌжБНгаДГіЕНдЕуOЕФ![]() ЕФГЄЖШЃЛ
ЕФГЄЖШЃЛ
ЂкШчЙћMNдкдВЩЯдЫЖЏЪБЃЌдкЭМ2жаЛГіЪОвтЭМЃЌВЂжБНгаДГіЕНЕуOЕФ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ЃЈ2ЃЉвбжЊЕу![]() ,ЕуNЮЊЁбWЩЯЕФвЛЖЏЕуЃЌгажБЯп
,ЕуNЮЊЁбWЩЯЕФвЛЖЏЕуЃЌгажБЯп![]() ЃЌЧѓЕНжБЯп
ЃЌЧѓЕНжБЯп![]() ЕФ
ЕФ![]() ЕФзюДѓжЕ.
ЕФзюДѓжЕ.
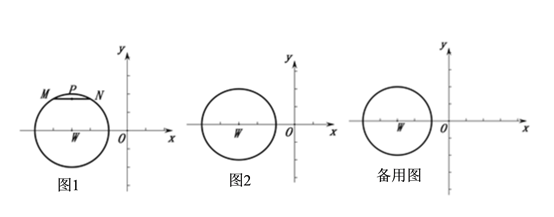
ЁОД№АИЁПЃЈ1ЃЉЂй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЃЈ2ЃЉdжаЕФзюДѓжЕЮЊ
ЃЛЃЈ2ЃЉdжаЕФзюДѓжЕЮЊ![]() .
.
ЁОНтЮіЁП
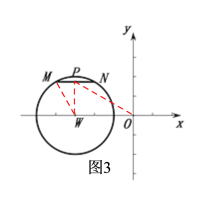
ЃЈ1ЃЉЂйШчЭМ3ЃЌСЌНгPWЁЂOPЁЂMWЃЌгЩвбжЊвзЕУPW=![]() ЃЌЁЯPWO=90ЁуЃЌOW=3ЃЌетбљдкRtЁїPWOжагЩЙДЙЩЖЈРэМДПЩЧѓЕУДЫЪБЕуPЕНдЕуOЕФЯвжаОрdжа=
ЃЌЁЯPWO=90ЁуЃЌOW=3ЃЌетбљдкRtЁїPWOжагЩЙДЙЩЖЈРэМДПЩЧѓЕУДЫЪБЕуPЕНдЕуOЕФЯвжаОрdжа=![]() ЃЛЂкгЩЬтвтПЩжЊЃЌЕБЯвMNдкЁбWЩЯдЫЖЏЪБЃЌЕуPЕФдЫЖЏТЗЯпЪЧвдЕуWЮЊдВаФЃЌPWЮЊАыОЖЕФдВЃЌШчЭМ4ЃЌЛГіЖдгІЕФЭМаЮЃЌгЩЭМНсКЯPW=
ЃЛЂкгЩЬтвтПЩжЊЃЌЕБЯвMNдкЁбWЩЯдЫЖЏЪБЃЌЕуPЕФдЫЖЏТЗЯпЪЧвдЕуWЮЊдВаФЃЌPWЮЊАыОЖЕФдВЃЌШчЭМ4ЃЌЛГіЖдгІЕФЭМаЮЃЌгЩЭМНсКЯPW=![]() ЃЌМДПЩЕУЕНДЫЪБЕуPЕНдЕуOЕФЯвжаОрdжаЕФШЁжЕЗЖЮЇСЫЃЛ
ЃЌМДПЩЕУЕНДЫЪБЕуPЕНдЕуOЕФЯвжаОрdжаЕФШЁжЕЗЖЮЇСЫЃЛ
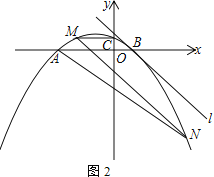
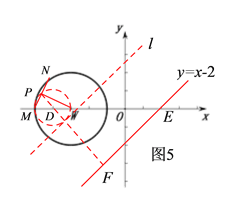
ЃЈ2ЃЉгЩЬтвтвзЕУЕБЕуNдкЁбWЩЯдЫЖЏЪБЃЌЕуPдквдDЮЊдВаФЃЌWMЮЊжБОЖЕФдВЩЯдЫЖЏЃЌгЩДЫЛГіЗћКЯЬтвтЕФЭМаЮШчЭМ5ЃЌзїжБЯпlЦНаагкжБЯпy=x-2ЃЌдђгЩЭМПЩжЊЃЌЕБжБЯпlгыЁбDЯрЧаЃЌЧвЯвжаОрdжаЙ§дВаФDЪБЃЌЕуPЕНжБЯпlЕФЯвжаОрdжазюДѓЃЌдђДЫЪБЕуPЕНжБЯпy=x-2ЕФЯвжаОрвВзюДѓЃЌетбљНсКЯвбжЊЬѕМўНјааМЦЫуМДПЩЧѓЕУЫљЧѓЕФжЕСЫ.
ЃЈ1ЃЉЂйШчЭМ3ЃЌСЌНгPWЁЂOPЁЂMWЃЌ
ЁпЕуPЪЧMNЕФжаЕуЃЌMN=2ЃЌ
ЁрPWЁЭMNЃЌMP=1ЃЌ
ЁпMNЁЮxжсЃЌ
ЁрPWЁЭxжсЃЌ
ЁрЁЯPWO=90ЁуЃЌ
ЁпOW=3ЃЌ
ЁрдкRtЁїPWOжаЃЌPO=![]() ЃЌ
ЃЌ
ЁрДЫЪБЕуPЕНдЕуOЕФЯвжаОрЃКdжа=![]() ЃЛ
ЃЛ
ЂкгЩЬтвтПЩжЊЃЌЕБЯвMNдкЁбWЩЯдЫЖЏЪБЃЌЕуPЕФдЫЖЏТЗЯпЪЧвдЕуWЮЊдВаФЃЌPWЮЊАыОЖЕФдВЃЌШчЭМ4ЃЌ
ЁпPW=![]() ЃЌOW=3ЃЌ
ЃЌOW=3ЃЌ
ЁрДЫЪБЕуPЕНдЕуOЕФЯвжаОрdжаЕФШЁжЕЗЖЮЇЮЊЃК![]() <dжа<
<dжа<![]() ЃЛ
ЃЛ

ЃЈ2ЃЉШчЭМ5ЃЌЁпPЪЧЯвMNЕФжаЕуЃЌ
ЁрWPЁЭMNЃЌ
ЁрЕБЕуNдкЁбWЩЯдЫЖЏЪБЃЌЕуPдквдDЮЊдВаФЃЌWMЮЊжБОЖЕФдВЩЯдЫЖЏЃЌ
ЁпWЕФзјБъЮЊЃЈ-3ЃЌ0ЃЉЃЌЕуMЕФзјБъЮЊЃЈ-5ЃЌ0ЃЉЃЌ
ЁрЕуDЕФзјБъЮЊЃЈ-4ЃЌ0ЃЉЃЌ
зїжБЯпlЦНаагкжБЯпy=x-2ЃЌдђЕБЕуPЕНжБЯпlЕФЯвжаОрзюДѓЪБЃЌЕуPЕНжБЯпy=x-2ЕФЯвжаОрОЭзюДѓЃЌ
гЩЭМПЩжЊЃЌЕБжБЯпlгыЁбDЯрЧаЃЌЧвЯвжаОрdжаЙ§дВаФDЪБЃЌЕуPЕНжБЯпlЕФЯвжаОрdжазюДѓЃЌ
ЩшжБЯпy=x-2гыxжсНЛгкЕуEЃЌЙ§ЕуDзїжБЯпy=x-2ЕФДЙЯпНЛжБЯпгкЕуFЃЌ
ЁпжБЯпy=x-2гыxжсЯрНЛаЮГЩЕФШёНЧЮЊ45ЁуЃЌЕуEЕФзјБъЮЊЃЈ2ЃЌ0ЃЉЃЌ
ЁрDE=6ЃЌ
ЁрDF=DEЁЄsin45Ёу=![]() ЃЌМДДЫЪБжБЯпlЕНжБЯпy=x-2ЕФОрРыЮЊ
ЃЌМДДЫЪБжБЯпlЕНжБЯпy=x-2ЕФОрРыЮЊ![]() ЃЌ
ЃЌ
ЁрЕуPЕНжБЯпy=x-2ЕФзюДѓОрРыЮЊЃК![]() ЃЌМДdжаЕФзюДѓжЕЮЊЃК
ЃЌМДdжаЕФзюДѓжЕЮЊЃК![]() .
.

ЁОЬтФПЁПЮЊСЫЙФРјОгУёНкдМгУЫЎЃЌФГЪаздРДЫЎЙЋЫОАДШчЯТЗНЪНЖдУПЛЇдТгУЫЎСПНјааМЦЫуЃКЕБгУЫЎСПВЛГЌЙ§![]() ЗНЪБЃЌУПЗНЕФЪеЗбБъзМЮЊ
ЗНЪБЃЌУПЗНЕФЪеЗбБъзМЮЊ![]() дЊЃЌЕБгУЫЎСПГЌЙ§
дЊЃЌЕБгУЫЎСПГЌЙ§![]() ЗНЪБЃЌГЌГі
ЗНЪБЃЌГЌГі![]() ЗНЕФВПЗжУПЗНЕФЪеЗбБъзМЮЊ
ЗНЕФВПЗжУПЗНЕФЪеЗбБъзМЮЊ![]() дЊЃЌЯТБэЪЧаЁУїМв
дЊЃЌЯТБэЪЧаЁУїМв![]() дТЗнгУЫЎСПКЭНЛЗбЧщПіЃК
дТЗнгУЫЎСПКЭНЛЗбЧщПіЃК
дТЗн |
|
|
|
|
гУЫЎСПЃЈЗНЃЉ |
|
|
|
|
ЗбгУЃЈдЊЃЉ |
|
|
|
|
ЧыИљОнБэИёжаЬсЙЉЕФаХЯЂЃЌЛиД№вдЯТЮЪЬтЃК
ЃЈ1ЃЉ![]() ___________ЃЎ
___________ЃЎ![]() ____________ЃЛ
____________ЃЛ
ЃЈ2ЃЉШєаЁУїМв![]() дТЗнНЛФЩЫЎЗб
дТЗнНЛФЩЫЎЗб![]() дЊЃЌдђаЁУїМв
дЊЃЌдђаЁУїМв![]() дТЗнгУЫЎЖрЩйЗНЃП
дТЗнгУЫЎЖрЩйЗНЃП
ЁОЬтФПЁПСавЛдЊвЛДЮЗНГЬНтгІгУЬтЃК
2019Фъ6дТвдРДжэШтМлИёВЛЖЯзпИпЃЌв§Ц№СЫУёжкгыеўИЎЕФИпЖШЙизЂЃЌЪаГЁжэШтЕФЕЅМлеЧЕНУПЧЇПЫ50дЊЪБЃЌеўИЎОіЖЈЭЖШыДЂБИжэШтвдЦНвжжэШтМлИёЃЎ2019Фъ12дТЃЌеўЖдЭЖЗХДЂБИжэШт4ЭђЖжЃЌЭЖЗХКѓУёжкПЊЪМДѓСПВЩЙКЃЌФГГЌЪавВзіСЫЯргІЕФДйЯњЛюЖЏШчЯТЃК
вЛДЮадЙКТђЪ§СПЃЈЧЇПЫЃЉ | ЗЕЛЙН№Жю |
ВЛГЌЙ§20ЧЇПЫ | вЛТЩАДЪлМлЗЕЛЙ |
ГЌЙ§20ЧЇПЫЃЌЕЋВЛГЌЙ§40ЧЇПЫ | вЛТЩАДЪлМлЗЕЛЙ |
ГЌЙ§40ЧЇПЫ | Г§АДЪлМлЗЕЛЙ |
Р§ШчЃКФГЙЫПЭТђСЫ45ЧЇПЫжэШтЃЌдђЪЕМЪИЖПюЮЊЃК![]() ЃЈдЊЃЉЃЎ
ЃЈдЊЃЉЃЎ
ЃЈ1ЃЉИУГЌЪадкДйЯњЧАЙКНјСЫвЛХњжэШтЃЌДйЯњЧАвдУПЧЇПЫ50дЊЕФЕЅМлТєГі10ЧЇПЫЃЌДйЯњЦкМфвдЭЌбљЕФЕЅМлТєСЫ30ЧЇПЫИјаЁУїМвЃЎНсЙћЗЂЯжЃЌДйЯњЧАТєГіЕФ10ЧЇПЫжэШтЛёЕУЕФРћШѓИњТєИјаЁУїМвЕФ30ЧЇПЫжэШтЛёЕУЕФРћШѓвЛбљЖрЃЌЧѓИУГЌЪаЙКНјетХњжэШтЕФНјМлЮЊУПЧЇПЫЖрЩйдЊЃП
ЃЈ2ЃЉДйЯњЦкМфЃЌаЁКьМвДгИУГЌЪавдУПЧЇПЫ50дЊЕФЕЅМлЗжСНДЮЙВЙКТђжэШт80ЧЇПЫЃЌЕквЛДЮЙКТђЕФЪ§СПЩйгкЕкЖўДЮЙКТђЕФЪ§СПЃЌШєСНДЮЪЕМЪЙВИЖПю2990дЊЃЌдђаЁКьМвСНДЮЗжБ№ЙКТђжэШтЖрЩйЧЇПЫЃП