题目内容
若AD为△ABC的高,AD=1,BD=1,DC=
,则∠BAC= .
| 3 |
考点:解直角三角形
专题:计算题
分析:在直角三角形ABD中,由AD=BD,得到三角形ABD为等腰直角三角形,求出∠BAD度数,在直角三角形ACD中,利用勾股定理求出AC的长,确定出∠DAC的度数,由∠BAD+∠DAC求出∠BAC度数即可.
解答: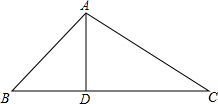 解:如图所示,
解:如图所示,
在Rt△ABD中,AD=BD=1,
∴△ABD为等腰直角三角形,即∠BAD=45°,
在Rt△ACD中,AD=1,CD=
,
根据勾股定理得:AC=2,
∴∠C=30°,即∠DAC=60°,
则∠BAC=∠BAD+∠DAC=105°.
同理,当AD在BC的延长线上时,∠BAC=15°.
故答案为:105°或15°.
 解:如图所示,
解:如图所示,在Rt△ABD中,AD=BD=1,
∴△ABD为等腰直角三角形,即∠BAD=45°,
在Rt△ACD中,AD=1,CD=
| 3 |
根据勾股定理得:AC=2,
∴∠C=30°,即∠DAC=60°,
则∠BAC=∠BAD+∠DAC=105°.
同理,当AD在BC的延长线上时,∠BAC=15°.
故答案为:105°或15°.
点评:此题考查了解直角三角形,等腰直角三角形的性质,勾股定理,熟练掌握直角三角形的性质是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F,若∠B=60°,∠C=70°,求∠EDF的度数.
如图,在△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F,若∠B=60°,∠C=70°,求∠EDF的度数. 如图,∠1=∠2=115°,∠3=65°,图中有哪些直线互相平行.
如图,∠1=∠2=115°,∠3=65°,图中有哪些直线互相平行. 如图所示,梯形ABCD中,AD∥BC,∠A=90°,AB=11,AD=3,BC=6,P为腰AB上一点,当AP为何值时,以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似?
如图所示,梯形ABCD中,AD∥BC,∠A=90°,AB=11,AD=3,BC=6,P为腰AB上一点,当AP为何值时,以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似? 如图,在矩形ABCD中,M是BC的中点,MA⊥MD,AB=4,求矩形ABCD的面积是
如图,在矩形ABCD中,M是BC的中点,MA⊥MD,AB=4,求矩形ABCD的面积是