题目内容
一个直角三角形的两条直角边相差5cm，面积是7cm2，则斜边的长是 cm．
考点：勾股定理
专题：
分析：设较短的直角边长是xcm，较长的就是（x+5）cm，根据面积是7cm2，求出直角边长，根据勾股定理求出斜边长．
解答：解：设较短的直角边长是xcm，较长的就是（x+5）cm，则
x•（x+5）=7，
整理得：x2+5x-14=0，
∴（x+7）（x-2）=0，
∴x=2或x=-7（舍去）．
∴5+2=7（cm），
∴由勾股定理，得
=
，即斜边的长是
cm．
故答案是：
．
| 1 |
| 2 |
整理得：x2+5x-14=0，
∴（x+7）（x-2）=0，
∴x=2或x=-7（舍去）．
∴5+2=7（cm），
∴由勾股定理，得
| 22+72 |
| 53 |
| 53 |
故答案是：
| 53 |
点评：本题考查了一元二次方程的应用，关键知道三角形面积公式以及直角三角形中勾股定理的应用．
练习册系列答案
相关题目
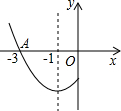如图是抛物线y=ax2+bx+c的一部分，其对称轴为直线x=-1，它与x轴的一个交点为A（-3，0），根据图象，可知一元二次方程ax2+bx+c=0的另一个解是
如图，在边长为1的正方形中，分别以四个顶点为圆心，作半径为1的圆弧，则图中阴影部分的面积是
如图，七个大小不等的圆，其中没能体现出圆与圆的位置关系是（ ）| A、外切 | B、内含 | C、相交 | D、内切 |
下列运算中，正确的是（ ）
A、3+
| ||||
B、1÷（2×
| ||||
C、42×（
| ||||
| D、39-6=39-36 |
