Question

【题目】如图，中，，顶点分别在反比例函数与的图象上，则的值为___________.

Answer 1

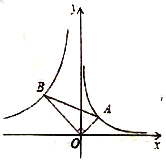
【答案】

【解析】

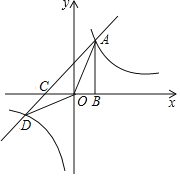
过A作AC⊥x轴，过B作BD⊥x轴于D，于是得到∠BDO=∠ACO=90°，根据反比例函数的性质得到S△BDO=5，S△AOC=1，根据相似三角形的性质得到=，根据三角函数的定义即可得到结论．

解：过A作AC⊥x轴，过B作BD⊥x轴于D，

则∠BDO=∠ACO=90°，

∵顶点A，B分别在反比例函数y=（x＞0）与y=（x＜0）的图象上，

∴S△BDO=5，S△AOC=1，

∵∠AOB=90°，

∴∠BOD+∠DBO=∠BOD+∠AOC=90°，

∴∠DBO=∠AOC，

∴△BDO∽△OCA，

∴，

∴，

∴tan∠BAO=，

故答案为：．