题目内容
 26、如图是某居民小区的一块长为2a米,宽为b米的长方形空地,为了美化环境,准备在这个长方形的四个顶点处修建一个半径为a米的扇形花台,然后在花台内种花,其余种草.如果建造花台及种花费用每平方米需要资金100元,种草每平方米需要资金50元,那么美化这块空地共需资金多少元?
26、如图是某居民小区的一块长为2a米,宽为b米的长方形空地,为了美化环境,准备在这个长方形的四个顶点处修建一个半径为a米的扇形花台,然后在花台内种花,其余种草.如果建造花台及种花费用每平方米需要资金100元,种草每平方米需要资金50元,那么美化这块空地共需资金多少元?分析:花台面积为πa2平方米,所需资金为πa2×100.草地面积为(2ab-πa2)平方米,所需资金为(2ab-πa2)×50.共需资金为花台所需资金+草地所需资金.
解答:解:100×πa2+50(2ab-πa2)=50πa2+100ab(元).
点评:本题考查列代数式.先求面积再求所需资金的和.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
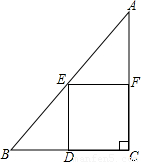
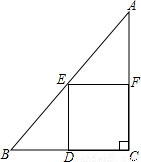
 块空地建一个矩形停车场DCFE,使得D点在BC边上,E、F分别是AB、AC边的中点.
块空地建一个矩形停车场DCFE,使得D点在BC边上,E、F分别是AB、AC边的中点.