Question

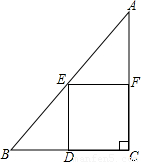
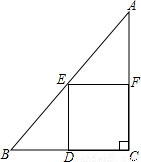
如图是某居民小区的一块直角三角形空地ABC，其斜边AB=100米，直角边AC=80米．
（1）求另一条直角BC的长度；
（2）现要利用这块空地建一个矩形停车场DCFE，使得D在BC边上，E、F分别是AB、AC边的中点．求矩形DCFE的面积；
（3）现要利用这块空地建一个正方形停车场DCFE，使得D点在BC边上，E、F分别是AB、AC边的点．求正方形DCFE的面积．

Answer 1

分析：（1）直接根据勾股定理求出BC的长即可；
（2）先根据三角形中位线定理求出EF的长，再根据矩形的面积公式求解即可；
（3）设正方形的边长为x，根据相似三角形的性质求出x的值，再由正方形的面积公式求解即可．

解答：解：（1）∵△ABC是直角三角形，其斜边AB=100米，直角边AC=80米．
∴BC=

AB2-AC2

=

1002-802

=60（米）；

（2）∵E、F分别是AB、AC边的中点，
∴EF=

1

2

BC=

1

2

×60=30（米），CF=

1

2

AC=

1

2

×80=40米，
∴S_矩形DCFE=CF•EF=40×30=1200平方米；

（3）设正方形的边长为x，
∵EF∥BC，
∴△AEF∽△ABC，
∴

AF

AC

=

EF

BC

，即

80-x

80

=

x

60

，解得x=

240

7

米，
∴S_{正方形DCFE}=EF•CF=（

240

7

）²=

57600

49

平方米．
答：正方形DCFE的面积为

57600

49

平方米．

点评：本题考查的是相似三角形的应用及勾股定理，熟知相似三角形的对应边成比例是解答此题的关键．