题目内容
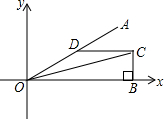 如图,∠AOC=∠BOC=15°,DC∥x轴,CB⊥x轴于点B,点D、B的横坐标分别为
如图,∠AOC=∠BOC=15°,DC∥x轴,CB⊥x轴于点B,点D、B的横坐标分别为 ,
, ,则点C的坐标为________.
,则点C的坐标为________.
(4+2 ,2)
,2)
分析:过点C作CE⊥OA于E,根据两直线平行,内错角相等求出∠CDE=30°,根据点D、B的横坐标求出CD的长,再根据直角三角形30°角所对的直角边等于斜边的一半求出CE,然后根据角平分线上的点到角的两边的距离相等可得CB=CE,即可得解.
解答: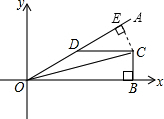 解:如图,过点C作CE⊥OA于E,
解:如图,过点C作CE⊥OA于E,
∵DC∥x轴,
∴∠CDE=∠AOB=15°+15°=30°,
∵点D、B的横坐标分别为2 ,4+2
,4+2 ,
,
∴CD=4+2 -2
-2 =4,
=4,
∴CE= CD=
CD= ×4=2,
×4=2,
又∵∠AOC=∠BOC=15°,CB⊥x轴,
∴CB=CE=2,
∴点C的坐标为(4+2 ,2).
,2).
故答案为:(4+2 ,2).
,2).
点评:本题考查了角平分线上的点到角的两边的距离相等的性质,直角三角形30°角所对的直角边等于斜边的一半的性质,熟记性质并作出辅助线是解题的关键.
 ,2)
,2)分析:过点C作CE⊥OA于E,根据两直线平行,内错角相等求出∠CDE=30°,根据点D、B的横坐标求出CD的长,再根据直角三角形30°角所对的直角边等于斜边的一半求出CE,然后根据角平分线上的点到角的两边的距离相等可得CB=CE,即可得解.
解答:
 解:如图,过点C作CE⊥OA于E,
解:如图,过点C作CE⊥OA于E,∵DC∥x轴,
∴∠CDE=∠AOB=15°+15°=30°,
∵点D、B的横坐标分别为2
 ,4+2
,4+2 ,
,∴CD=4+2
 -2
-2 =4,
=4,∴CE=
 CD=
CD= ×4=2,
×4=2,又∵∠AOC=∠BOC=15°,CB⊥x轴,
∴CB=CE=2,
∴点C的坐标为(4+2
 ,2).
,2).故答案为:(4+2
 ,2).
,2).点评:本题考查了角平分线上的点到角的两边的距离相等的性质,直角三角形30°角所对的直角边等于斜边的一半的性质,熟记性质并作出辅助线是解题的关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
 25、如图,△AOC≌△BOD,试证明AC∥BD.
25、如图,△AOC≌△BOD,试证明AC∥BD. 22、证明:角的平分线上的点到角的两边的距离相等.
22、证明:角的平分线上的点到角的两边的距离相等.
 如图,∠AOC=140°,∠CBD=
如图,∠AOC=140°,∠CBD= 如图,∠AOC与∠BOD都是直角,且射线OB平分∠AOC,∠DOA的度数等于( )
如图,∠AOC与∠BOD都是直角,且射线OB平分∠AOC,∠DOA的度数等于( )