题目内容
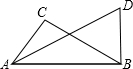
在矩形ABCD中,CE⊥BD,E为垂足,连接AE,已知BC=3,CD=4,
求(1)△ADE的面积;
(2)tan∠EAB.

求(1)△ADE的面积;
(2)tan∠EAB.

如图:
(1)∵BC=3,CD=4
∴BD=5,CE=
在直角三角形BCE中,
BE=
•
=
∴DE=BD-BE=
∴△ADE的面积为
•DE•CE=
.
(2)过E作EF⊥AB,
∴EF=BE•
=
,BF=BE•
=
∴AF=AB-BF=
∴tan∠EAB=
=
.

(1)∵BC=3,CD=4
∴BD=5,CE=
| 12 |
| 5 |
在直角三角形BCE中,
BE=
| 3 |
| 4 |
| 12 |
| 5 |
| 9 |
| 5 |
∴DE=BD-BE=
| 16 |
| 5 |
∴△ADE的面积为
| 1 |
| 2 |
| 96 |
| 25 |
(2)过E作EF⊥AB,
∴EF=BE•
| 3 |
| 5 |
| 27 |
| 25 |
| 4 |
| 5 |
| 36 |
| 25 |
∴AF=AB-BF=
| 64 |
| 25 |
∴tan∠EAB=
| EF |
| AF |
| 27 |
| 64 |


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 为60米,山坡AC的坡度i=1:1.(提示:坡面的铅直高度与水平宽度的比称为坡度)
为60米,山坡AC的坡度i=1:1.(提示:坡面的铅直高度与水平宽度的比称为坡度)
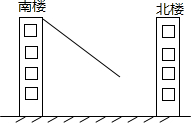

 染半径为100米,试问A、B两栋教室是否受到拖拉机噪声的影响若有影响,影响的时间有多少秒?(计算过程中
染半径为100米,试问A、B两栋教室是否受到拖拉机噪声的影响若有影响,影响的时间有多少秒?(计算过程中