Question

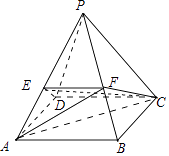
【题目】已知四棱锥P﹣ABCD，底面ABCD为矩形，点E，F在侧棱PA，PB上且PE=2EA，PF=2FB，点M为四棱锥内任一点，则M在平面EFCD上方的概率是（ ）
A.
B.
C.
D.

Answer 1

【答案】B
【解析】解：如图，设四棱锥P﹣ABCD的高为h，底面ABCD的面积为S， ∴ ．

∵PE=2EA，PF=2FB，
∴EF∥AB，则EF∥平面ABCD，且F到平面ABCD的距离为 ，
∴ ，
， = ．
则多面体ABCDEF的体积为 ．
∴ ．
∴M在平面EFCD上方的概率是 ．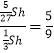
故选：B．
【考点精析】本题主要考查了几何概型的相关知识点，需要掌握几何概型的特点：1）试验中所有可能出现的结果（基本事件）有无限多个；2）每个基本事件出现的可能性相等才能正确解答此题．