题目内容
在菱形ABCD中,对角线AC与BD相交于点O,AB=5,AC=6.过D点作DE∥AC交BC的延长线于点E.
(1)求△BDE的周长;
(2)点P为线段BC上的点,连接PO并延长交AD于点Q.求证:BP=DQ.

(1)解:∵四边形ABCD是菱形,
∴AB=BC=CD=AD=5,AC⊥BD,OB=OD,OA=OC=3
∴![]() ,BD=2OB=8
,BD=2OB=8
∵AD∥CE,AC∥DE,∴四边形ACED是平行四边形
∴CE=AD=BC=5,DE=AC=6
∴△BDE的周长是:BD+BC+CE+DE=8+10+6=24.
(2)证明:∵AD∥BC,∴∠OBP=∠ODQ,∠OPD=∠OQD
∵OB=OD,∴△BOP≌△DOQ,∴BP=DQ。

练习册系列答案
相关题目
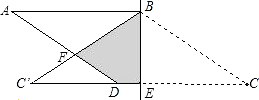 如图,在菱形ABCD中,BE⊥CD于点E,AB=5,BE=3,把菱形沿着BE对折,使点C落在点C′处,则重叠部分(即阴影部分)的面积是
如图,在菱形ABCD中,BE⊥CD于点E,AB=5,BE=3,把菱形沿着BE对折,使点C落在点C′处,则重叠部分(即阴影部分)的面积是 (2012•玉林)如图,在菱形ABCD中,对角线AC,BD相交于点O,且AC≠BD,则图中全等三角形有( )
(2012•玉林)如图,在菱形ABCD中,对角线AC,BD相交于点O,且AC≠BD,则图中全等三角形有( ) (2012•百色)如图,在菱形ABCD中,E、F是对角线AC上的两点,且AE=CF.
(2012•百色)如图,在菱形ABCD中,E、F是对角线AC上的两点,且AE=CF.
