题目内容
如图,反比例函数y= 的图象与一次函数y=kx+b的图象交于点A(m,2),点B(-2,n),一次函数图象与y轴的交点为C.
的图象与一次函数y=kx+b的图象交于点A(m,2),点B(-2,n),一次函数图象与y轴的交点为C.
 (1)求一次函数解析式;
(1)求一次函数解析式;
(2)求C点的坐标;
(3)求△AOC的面积.
解:(1)由题意,把A(m,2),B(-2,n)代入 中,得
中,得 ,
,
∴A(1,2),B(-2,-1)将A、B代入y=kx+b中得:
 ,∴
,∴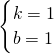 ,
,
∴一次函数解析式为:y=x+1;
(2)由(1)可知:当x=0时,y=1,
∴C(0,1);
(3)S△AOC= ×1×1=
×1×1= .
.
分析:(1)首先由反比例函数的解析式分别求得m、n的值,再进一步根据点A、B的坐标求得一次函数的解析式;
(2)根据(1)中求得的解析式,令x=0,即可求得点C的坐标;
(3)根据点A、C的坐标即可求得OC=1,OC边上的高是点A的横坐标,进一步求得三角形的面积.
点评:本题考查了反比例函数的综合应用,重点是由交点坐标求得函数的解析式,题目较难,同学们要重点掌握.
 中,得
中,得 ,
,∴A(1,2),B(-2,-1)将A、B代入y=kx+b中得:
 ,∴
,∴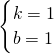 ,
,∴一次函数解析式为:y=x+1;
(2)由(1)可知:当x=0时,y=1,
∴C(0,1);
(3)S△AOC=
 ×1×1=
×1×1= .
.分析:(1)首先由反比例函数的解析式分别求得m、n的值,再进一步根据点A、B的坐标求得一次函数的解析式;
(2)根据(1)中求得的解析式,令x=0,即可求得点C的坐标;
(3)根据点A、C的坐标即可求得OC=1,OC边上的高是点A的横坐标,进一步求得三角形的面积.
点评:本题考查了反比例函数的综合应用,重点是由交点坐标求得函数的解析式,题目较难,同学们要重点掌握.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 如图,反比例函数y=
如图,反比例函数y= 如图,反比例函数
如图,反比例函数 如图,反比例函数
如图,反比例函数 如图,反比例函数
如图,反比例函数 如图,反比例函数
如图,反比例函数