Question

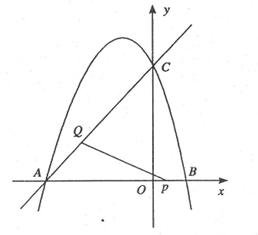
(本题20分) (湖南湘西,25,20分)如图.抛物线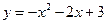与x轴相交于点A和点B,与y轴交于点C.
(1)求点A、点B和点C的坐标.
(2)求直线AC的解析式.
(3)设点M是第二象限内抛物线上的一点,且=6,求点M的坐标.
(4)若点P在线段BA上以每秒1个单位长度的速度从A运动(不与B,A重合),同时,点Q在射线AC上以每秒2个单位长度的速度从A向C运动.设运动的时间为t秒,请求出△APQ的面积S与t的函数关系式,并求出当t为何值时, △APQ的面积最大,最大面积是多少?

Answer 1

(1)令,(x+3)(x-1)=0,
A(-3,0)  B.(1,0),C(0,3)
(2)设直线AC的解析式为y=kx+b
由题意,得  解之得,y=x+3.
(3)设M点的坐标为(x,)
AB=4,因为M在第二象限,所以>0,
所以=6
解之,得,
当x=0时,y=3(不合题意)
当x=-2时,y=3.所以M点的坐标为(-2,3)
(4)由题意,得AB=4,PB=4-t,
∵AO=3,CO=3,
∴△ABC是等腰直角三角形,
AQ=2t,
所以Q点的纵坐标为t,
S=(1<t<4)

当t=2时△APQ最大,最大面积是解析:
略