题目内容
王磊同学设计了如图所示的图案，他设计的方案是：在△ABC中，AB=AC=6 cm，∠B=30°，以A为圆心，以AB长为半径作 |
| BEC |
|
| BDC |
分析：图案的面积即是半圆的面积+S△ABC-扇形的面积，利用面积公式计算即可，但在计算时要先解直角三角形计算出BC的长，和∠A的度数．
解答：解：∵AB=AC=6 cm，∠ABC=30°，
∴∠BAC=120°，BC=6
，A到BC的距离为3．
∴S扇形BAC=12πcm2；
S△ABC=9
cm2；
S半圆BDC=
π×(3
)2=
π．
∴S阴=S半圆BDC+S△ABC-S扇形BAC=(
π+9
)cm2．
∴∠BAC=120°，BC=6
| 3 |
∴S扇形BAC=12πcm2；
S△ABC=9
| 3 |
S半圆BDC=
| 1 |
| 2 |
| 3 |
| 27 |
| 2 |
∴S阴=S半圆BDC+S△ABC-S扇形BAC=(
| 3 |
| 2 |
| 3 |
点评：本题综合考查了解直角三角形和计算扇形的面积的能力，关键是得到所求的面积的等量关系．
练习册系列答案
相关题目
王磊同学设计了如图所示的图案，他设计的方案是：在△ABC中，AB=AC=6 cm，∠B=30°，以A为圆心，以AB长为半径作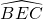
；以BC为直径作
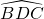，则该图案的面积是多少？
；以BC为直径作
，则该图案的面积是多少？