题目内容
 (2013•济宁)如图,矩形ABCD的面积为20cm2,对角线交于点O;以AB、AO为邻边做平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边做平行四边形AO1C2B;…;依此类推,则平行四边形AO4C5B的面积为( )
(2013•济宁)如图,矩形ABCD的面积为20cm2,对角线交于点O;以AB、AO为邻边做平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边做平行四边形AO1C2B;…;依此类推,则平行四边形AO4C5B的面积为( )分析:根据矩形的对角线互相平分,平行四边形的对角线互相平分可得下一个图形的面积是上一个图形的面积的
,然后求解即可.
| 1 |
| 2 |
解答: 解:设矩形ABCD的面积为S=20cm2,
解:设矩形ABCD的面积为S=20cm2,
∵O为矩形ABCD的对角线的交点,
∴平行四边形AOC1B底边AB上的高等于BC的
,
∴平行四边形AOC1B的面积=
S,
∵平行四边形AOC1B的对角线交于点O1,
∴平行四边形AO1C2B的边AB上的高等于平行四边形AOC1B底边AB上的高的
,
∴平行四边形AO1C2B的面积=
×
S=
,
…,
依此类推,平行四边形AO4C5B的面积=
=
=
cm2.
故选B.
 解:设矩形ABCD的面积为S=20cm2,
解:设矩形ABCD的面积为S=20cm2,∵O为矩形ABCD的对角线的交点,
∴平行四边形AOC1B底边AB上的高等于BC的
| 1 |
| 2 |
∴平行四边形AOC1B的面积=
| 1 |
| 2 |
∵平行四边形AOC1B的对角线交于点O1,
∴平行四边形AO1C2B的边AB上的高等于平行四边形AOC1B底边AB上的高的
| 1 |
| 2 |
∴平行四边形AO1C2B的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| S |
| 22 |
…,
依此类推,平行四边形AO4C5B的面积=
| S |
| 25 |
| 20 |
| 25 |
| 5 |
| 8 |
故选B.
点评:本题考查了矩形的对角线互相平分,平行四边形的对角线互相平分的性质,得到下一个图形的面积是上一个图形的面积的
是解题的关键.
| 1 |
| 2 |

练习册系列答案
相关题目
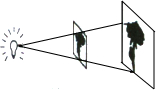 (2013•济宁)如图,放映幻灯时,通过光源,把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为
(2013•济宁)如图,放映幻灯时,通过光源,把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为 (2013•济宁)如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是( )
(2013•济宁)如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是( )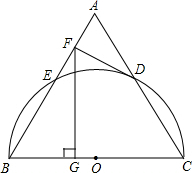 (2013•济宁)如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为( )
(2013•济宁)如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为( )