题目内容
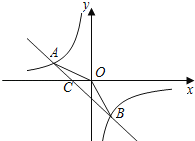
【题目】如图,在平面直角坐标系xOy中,若点A(﹣2,n),B(1,﹣2)是一次函数y=kx+b的图象和反比例函数y=![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标;
(3)求点O到直线AB的距离.
【答案】(1)反比例函数的解析式为y=﹣![]() ,一次函数的解析式为y=﹣x﹣1;(2)点C(﹣1,0);(3)点O到直线AB的距离为
,一次函数的解析式为y=﹣x﹣1;(2)点C(﹣1,0);(3)点O到直线AB的距离为![]() .
.
【解析】试题分析:(1)根据点B的坐标求出反比例函数解析式,根据反比例函数得出点A的坐标,最后根据A、B的坐标得出一次函数解析式;(2)令y=0得出点C的坐标;(3)利用面积法求出点O到直线的距离.
试题解析:(1)∵点B(1,-2)在函数y=![]() 的图象上,∴
的图象上,∴![]() , 得:m=-2.
, 得:m=-2.
∴反比例函数的解析式为y=-![]() .
.
∵点A(-2,n)在函数y=-![]() 的图象上, ∴
的图象上, ∴![]() 得:n=1.∴A(-2,1)
得:n=1.∴A(-2,1)
∵y=kx+b经过点A和点B ∴![]() 解得:
解得: ![]()
∴一次函数的解析式为y=-x-1.
(2)在一次函数的解析式y=-x-1中,令y=0得x=-1.∴点C的坐标为(-1,0).
(3)设点![]() 到直线AB的距离为
到直线AB的距离为![]() 直线AB与
直线AB与![]() 轴相交于
轴相交于![]() ,则
,则![]() .
.
则: ![]() .
. ![]()
![]() 点
点![]() 到直线AB的距离为
到直线AB的距离为![]() .
.

练习册系列答案
相关题目

