题目内容
如图,AE是△ABC中BC边上的高线也是中线,点D在线段AE上(不与两端点重合).(1)证明:△ADB≌△ADC;
(2)当△AEB∽△BED时,若sin∠BAE=
 ,BC=4,求线段DE的长度.
,BC=4,求线段DE的长度.
【答案】分析:(1)由已知证明AE垂直平分线段BC,根据垂直平分线的性质得AB=AC,DB=DC,而AD=AD,利用“SSS”证明△ADB≌△ADC;
(2)由△AEB∽△BED得∠DBE=∠BAE,把问题转化到Rt△BDE中,解直角三角形求DE.
解答:(1)证明:∵AE是△ABC中BC边上的高线也是中线,即线段AE在BC的中垂线上,
∴AB=AC,DB=DC,
又∵AD=AD,
∴△ADB≌△ADC(SSS);
(2)解:∵△AEB∽△BED,∴∠BAE=∠DBE,
∵sin∠BAE= ,
,
∴sin∠DBE= ,
,
在Rt△DBE中,sin∠DBE= =
= ,
,
∴BD=3DE,
又BC=4,E为中点,∴BE=2,
∵DE2+BE2=BD2,∴DE2+4=9DE2,
解得 DE= .
.
点评:本题考查了相似三角形的判定与性质,全等三角形的判定与性质,解直角三角形.关键是根据题意得出线段的垂直平分线.
(2)由△AEB∽△BED得∠DBE=∠BAE,把问题转化到Rt△BDE中,解直角三角形求DE.
解答:(1)证明:∵AE是△ABC中BC边上的高线也是中线,即线段AE在BC的中垂线上,
∴AB=AC,DB=DC,
又∵AD=AD,
∴△ADB≌△ADC(SSS);
(2)解:∵△AEB∽△BED,∴∠BAE=∠DBE,
∵sin∠BAE=
 ,
,∴sin∠DBE=
 ,
,在Rt△DBE中,sin∠DBE=
 =
= ,
,∴BD=3DE,
又BC=4,E为中点,∴BE=2,
∵DE2+BE2=BD2,∴DE2+4=9DE2,
解得 DE=
 .
.点评:本题考查了相似三角形的判定与性质,全等三角形的判定与性质,解直角三角形.关键是根据题意得出线段的垂直平分线.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 如图,AE是△ABC的中线,F在AE上,AE=3AF,BF延长线交AC于点D.若△ABC的面积是48,求△AFD的面积.
如图,AE是△ABC的中线,F在AE上,AE=3AF,BF延长线交AC于点D.若△ABC的面积是48,求△AFD的面积.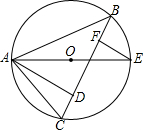 如图,AE是△ABC外接圆O的直径,AD是△ABC的边BC上的高,EF⊥BC,F为垂足.
如图,AE是△ABC外接圆O的直径,AD是△ABC的边BC上的高,EF⊥BC,F为垂足. (2012•梧州)如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=128°,∠C=36°,则∠DAE的度数是( )
(2012•梧州)如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=128°,∠C=36°,则∠DAE的度数是( ) 如图,AE是△ABC的中线,已知EC=6,DE=2,则BD的长为( )
如图,AE是△ABC的中线,已知EC=6,DE=2,则BD的长为( ) 如图,AE是△ABC的中线,A、E、D三点在一直线上,且AE=DE,那么△BDE可以看做是由
如图,AE是△ABC的中线,A、E、D三点在一直线上,且AE=DE,那么△BDE可以看做是由