题目内容
已知：如图，点
在以
为直径的⊙
上，点
在的延长线上，
.
(1)求证：
为⊙的切线；
(2) 过点作
于
.若
,求AD的长. （改编）
（1）证明：连接
. ---------------------------------1分
∵ 是⊙O直径，
∴ 
.∵ 
，
∴ 
． ∵ 
， ∴ 
.
即
.∴ 
.
又∵ 
是⊙O半径，∴ 为⊙的切线．-------------------------3分
（2）∵ 于，∴ 
.
∵ 于，∴ 
.∴ 
.
∴
.--------------------------4分
在△
中，，∴ 
，
∵ 
，
，∴ 
．
∴ 
．∴ ⊙的半径为
.--------------------------5分
∴ OD=
, AD=
练习册系列答案
相关题目
的抛物线
与
、点
，与
轴交于点
．
，使四边形
为等腰梯形，写出点
的解析式；
，抛物线上有一动点
，
．是否存在以
为顶点的平行四边形？如果存在，请直接写出点
中，
，点
在
上，以
长为半径的圆与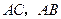
分别交于点
，且
．
与
的位置关系，并证明你的结论；
，
，求
的值．
中，
，
，
，以
为直径的⊙O交
于点
，点
是
的中点，OB，DE相交于点F。
是⊙O的切线；
在以
为直径的⊙
上，点
在
.
为⊙
于
.若
,求⊙