题目内容
 (2013•达州)如图,一条公路的转变处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600米,E为弧CD上一点,且OE⊥CD,垂足为F,OF=300
(2013•达州)如图,一条公路的转变处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600米,E为弧CD上一点,且OE⊥CD,垂足为F,OF=300| 3 |
分析:设这段弯路的半径为R米,OF=300
米,由垂径定理得CF=
CD=
×600=300.由勾股定理可得OC2=CF2+OF2,解得R的值,进而得出这段弧所对圆心角,求出弧长即可.
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:设这段弯路的半径为R米
解:设这段弯路的半径为R米
OF=300
米,
∵OE⊥CD
∴CF=
CD=
×600=300
根据勾股定理,得OC2=CF2+OF2
即R2=3002+(300
)2
解之,得R=600,
∴sin∠COF=
=
,
∴∠COF=30°,
∴这段弯路的长度为:
=200π(m).
故选:A.
 解:设这段弯路的半径为R米
解:设这段弯路的半径为R米OF=300
| 3 |
∵OE⊥CD
∴CF=
| 1 |
| 2 |
| 1 |
| 2 |
根据勾股定理,得OC2=CF2+OF2
即R2=3002+(300
| 3 |
解之,得R=600,
∴sin∠COF=
| FC |
| CO |
| 1 |
| 2 |
∴∠COF=30°,
∴这段弯路的长度为:
| 60π×600 |
| 180 |
故选:A.
点评:此题主要考查了垂径定理的应用,根据已知得出圆的半径以及圆心角是解题关键.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
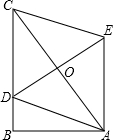 (2013•达州)如图,在Rt△ABC中,∠B=90°,AB=3,BC=4,点D在BC上,以AC为对角线的所有?ADCE中,DE最小的值是( )
(2013•达州)如图,在Rt△ABC中,∠B=90°,AB=3,BC=4,点D在BC上,以AC为对角线的所有?ADCE中,DE最小的值是( ) (2013•达州)如图,折叠矩形纸片ABCD,使B点落在AD上一点E处,折痕的两端点分别在AB、BC上(含端点),且AB=6,BC=10.设AE=x,则x的取值范围是
(2013•达州)如图,折叠矩形纸片ABCD,使B点落在AD上一点E处,折痕的两端点分别在AB、BC上(含端点),且AB=6,BC=10.设AE=x,则x的取值范围是 (2013•达州)如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2012BC和∠A2012CD的平分线交于点A2013,则∠A2013=
(2013•达州)如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2012BC和∠A2012CD的平分线交于点A2013,则∠A2013=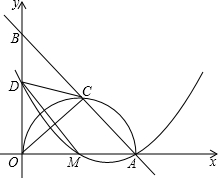 (2013•达州)如图,在平面直角坐标系中,直线AB交x轴于点A(5,0),交y轴于点B,AO是⊙M的直径,其半圆交AB于点C,且AC=3.取BO的中点D,连接CD、MD和OC.
(2013•达州)如图,在平面直角坐标系中,直线AB交x轴于点A(5,0),交y轴于点B,AO是⊙M的直径,其半圆交AB于点C,且AC=3.取BO的中点D,连接CD、MD和OC.