题目内容
已知，∠AOB=25°，OC⊥OA，OD⊥OB，则∠COD等于（ ）
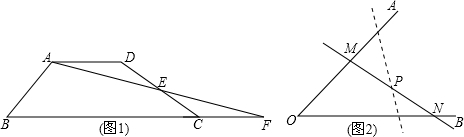
分析：分类讨论：如图1、2所示．根据图中相关角与角间的和差关系进行求解即可．
解答：
解：∵OC⊥OA，OD⊥OB，
∴∠AOC=90°，∠BOD=90°．
如图1，∠AOD=∠BOD-∠AOB=90°-25°=65°，
则∠COD=∠AOD+∠AOC=65°+90°=155°；
如图2，∠BOC=∠AOC-∠AOB=90°-25°=65°，
∠COD=∠BOD-∠BOC=90°-65°=25°．
综上所述，∠COD等于155°或25°．
故选D．
解：∵OC⊥OA，OD⊥OB，∴∠AOC=90°，∠BOD=90°．
如图1，∠AOD=∠BOD-∠AOB=90°-25°=65°，
则∠COD=∠AOD+∠AOC=65°+90°=155°；
如图2，∠BOC=∠AOC-∠AOB=90°-25°=65°，
∠COD=∠BOD-∠BOC=90°-65°=25°．
综上所述，∠COD等于155°或25°．
故选D．
点评：本题考查了垂线的定义．要注意领会由垂直得直角这一要点．
练习册系列答案
相关题目
如图，梯形ABCD两腰DA，CB的延长线交于O．已知S△AOB=4，S△AOC=9，则S梯形ABCD=（ ）| A、25 | B、16.25 | C、16 | D、15.25 |
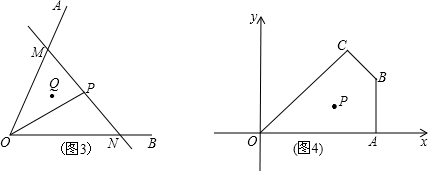
≈1.73）
，
）、（4、2），过点p的直线l与四边形OABC一组对边相交，将四边形OABC分成两个四边形，求其中以点O为顶点的四边形面积的最大值．