Question

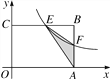
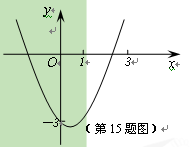
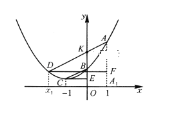
【题目】如图，已知点A（1，yA），B（0，yB），C（-1，yC），D（x1，yD）（x1≠1）在抛物线上，且AD//BC，AA1轴于A1，DF⊥AAl于F，CE⊥轴于E．

（1）求证：△ADF∽△BCE；

（2）当，，时，求的值；

（3）的值会随a，b，c的值改变而改变吗?若会，请求出与a，b，c的关系式；若不会，请说明理由．

Answer 1

【答案】（1）证明见解析；（2）-2；（3）不会，理由见解析.

【解析】

（1）由平行可得∠ADF=∠BCE, 又∵∠AFD=∠BEC=90°，可证△ADF∽△BCE，

（2）将a，b，c的值代入解析式求得y=，再由点B,C求得=3,因为AD//BC，则==3,从而可得直线AD的解析式，最后再求出直线与抛物线的交点即可.

（3）分别将A，B，C，代入，表示出A，B，C的坐标，同（2）表示出=(b-a)x+2a+c, 最后再求出直线与抛物线的交点为定值可知的值不会随a，b，c的值改变而改变.

解：（1）∵AD//BC，

∠ADF=∠DBC,

又∵DF∥CE,

∴∠DBC=∠BCE,

∴∠ADF=∠BCE,

又∵∠AFD=∠BEC=90°，

∴△ADF∽△BCE，

（2）当，，时，

∴y=，

∴A（1，15）；B（0，10）；C（-1，7），

设直线BC的解析式为：y=kx+b,将B（0，10），C（-1，7）代入得，

，解得，，

∵AD//BC，

∴可设直线AD的解析式为：=3x+m,将A（1，15）代入得，

15=3+m, 解得，m=12,

∴=3x+12,

∴ ，

解得， ，，

∴D（-2，6），

∴ ，

（3）不会，理由如下：

将A（1，yA），B（0，yB），C（-1，yC），代入，

得yA=a+b+c, yB=c, yC= a-b+c,

∴A（1，a+b+c,），B（0，c），C（-1，a-b+c），

∴==b-a,

∵AD//BC，

∴可设直线AD的解析式为：=(b-a)x +n,将A（1，a+b+c）代入得，

a+b+c=b-a +n,解得，n=2a+c,

∴=(b-a)x+2a+c,

∴,

化简得， ，

∴，

解得，=1（舍），=-2，

∴的值不会随a，b，c的值改变而改变.